题目内容
设正方形 ABCD,点P在线段CD的延长线上,且P点到A点的距离为1,那么,四边形ABCP的面积的最大可能值是
- A.
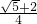
- B.

- C.

- D.
A
分析:由于直角三角形ADP的斜边长是1,所以设直角边AD=sinx (0<x< ),则把四边形ABCP的面积表示成三角函数形式;然后利用三角函数的有关公式(特别是asinx+bcosx=
),则把四边形ABCP的面积表示成三角函数形式;然后利用三角函数的有关公式(特别是asinx+bcosx= sin(x+φ)),把其转化为正弦型函数;最后根据正弦函数的值域,求得四边形ABCP面积的最大值.
sin(x+φ)),把其转化为正弦型函数;最后根据正弦函数的值域,求得四边形ABCP面积的最大值.
解答: 解:据题意画图如下
解:据题意画图如下
∵AP=1∴0<AD<1∴设AD=sinx (0<x< ).
).
则PD=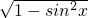 =cosx
=cosx
∴SABCP=sin2x+ sinxcosx=
sinxcosx= (1-cos2x)+
(1-cos2x)+ sin2x
sin2x
=( sin2x-
sin2x- cos2x)+
cos2x)+ =
= sin(2x-φ)+
sin(2x-φ)+
∴四边形ABCP的面积的最大值是 +
+ ,即
,即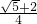 .
.
故选A.
点评:当有些数据在[-1,1]内时,可利用三角知识把它设为sinα或cosα的形式,然后充分利用三角函数的有关知识进行化简、运算,直至解决.否则问题可能会非常麻烦,甚至无法解决.
分析:由于直角三角形ADP的斜边长是1,所以设直角边AD=sinx (0<x<
 ),则把四边形ABCP的面积表示成三角函数形式;然后利用三角函数的有关公式(特别是asinx+bcosx=
),则把四边形ABCP的面积表示成三角函数形式;然后利用三角函数的有关公式(特别是asinx+bcosx= sin(x+φ)),把其转化为正弦型函数;最后根据正弦函数的值域,求得四边形ABCP面积的最大值.
sin(x+φ)),把其转化为正弦型函数;最后根据正弦函数的值域,求得四边形ABCP面积的最大值.解答:
 解:据题意画图如下
解:据题意画图如下∵AP=1∴0<AD<1∴设AD=sinx (0<x<
 ).
).则PD=
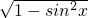 =cosx
=cosx∴SABCP=sin2x+
 sinxcosx=
sinxcosx= (1-cos2x)+
(1-cos2x)+ sin2x
sin2x=(
 sin2x-
sin2x- cos2x)+
cos2x)+ =
= sin(2x-φ)+
sin(2x-φ)+
∴四边形ABCP的面积的最大值是
 +
+ ,即
,即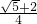 .
.故选A.
点评:当有些数据在[-1,1]内时,可利用三角知识把它设为sinα或cosα的形式,然后充分利用三角函数的有关知识进行化简、运算,直至解决.否则问题可能会非常麻烦,甚至无法解决.

练习册系列答案
相关题目
设正方形 ABCD,点P在线段CD的延长线上,且P点到A点的距离为1,那么,四边形ABCP的面积的最大可能值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

 如图,将正方形ABCD沿对角线BD折成直二面角,连接A′C得到三棱锥A′-BCD,A′F 垂直BD于F,E为BC的中点.
如图,将正方形ABCD沿对角线BD折成直二面角,连接A′C得到三棱锥A′-BCD,A′F 垂直BD于F,E为BC的中点. ,求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率。
,求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率。 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
.
 ;
; ;
;
 ∥
∥
 ∥DF,且AE=DF
∥DF,且AE=DF  AD∥EF
AD∥EF
 又
又



 为二面角A-BC-E的平面角,所以
为二面角A-BC-E的平面角,所以
 四边形ABCD是正方形
四边形ABCD是正方形