题目内容
 如图,将正方形ABCD沿对角线BD折成直二面角,连接A′C得到三棱锥A′-BCD,A′F 垂直BD于F,E为BC的中点.
如图,将正方形ABCD沿对角线BD折成直二面角,连接A′C得到三棱锥A′-BCD,A′F 垂直BD于F,E为BC的中点.(1)求证:EF∥平面A′CD
(2)设正方形ABCD边长为a,求折后所得三棱锥A′-BCD的侧面积.
分析:(1)根据题意,F为BD的中点.又E为BC的中点,可得EF∥CD.再根据直线和平面平行的判定定理证得EF∥平面A′CD.
(2)连接CFCF,根据AA′F⊥平面BCD,可得∠A′FC=90°,△A′BC和△A′DC都为边长为a的等边三角形,再根据S侧=SA′BD+SA′BC+SA′CD,运算求得结果
(2)连接CFCF,根据AA′F⊥平面BCD,可得∠A′FC=90°,△A′BC和△A′DC都为边长为a的等边三角形,再根据S侧=SA′BD+SA′BC+SA′CD,运算求得结果
解答:解: (1)证明:根据题意,有平面A′BD⊥平面BCD,由于A′F⊥BD于F,A′D=A′B,∴F为BD的中点.
(1)证明:根据题意,有平面A′BD⊥平面BCD,由于A′F⊥BD于F,A′D=A′B,∴F为BD的中点.
又∵E为BC的中点,∴EF∥CD.
再根据CD?平面A′CD,而EF不在平面A′CD 内,
∴EF∥平面A′CD.
(2)连接CF,∵平面A′BD⊥平面BCD,A′F⊥BD,
∴A′F⊥平面BCD,∴∠A′FC=90°.
∴A′C2=A′F2+FC2=(
a)2+(
a)2=a2.
∴△A′BC和△A′DC都为边长为a的等边三角形.
∴S侧=SA′BD+SA′BC+SA′CD=
•
a•
a+
a2+
a2 =
a2.
 (1)证明:根据题意,有平面A′BD⊥平面BCD,由于A′F⊥BD于F,A′D=A′B,∴F为BD的中点.
(1)证明:根据题意,有平面A′BD⊥平面BCD,由于A′F⊥BD于F,A′D=A′B,∴F为BD的中点.又∵E为BC的中点,∴EF∥CD.
再根据CD?平面A′CD,而EF不在平面A′CD 内,
∴EF∥平面A′CD.
(2)连接CF,∵平面A′BD⊥平面BCD,A′F⊥BD,
∴A′F⊥平面BCD,∴∠A′FC=90°.
∴A′C2=A′F2+FC2=(
| ||
| 2 |
| ||
| 2 |
∴△A′BC和△A′DC都为边长为a的等边三角形.
∴S侧=SA′BD+SA′BC+SA′CD=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
1+
| ||
| 2 |
点评:本题主要考查直线和平面平行的判定定理的应用,求棱锥的表面积,属于中档题.

练习册系列答案
相关题目
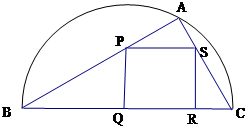 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
 如图,已知正方形ABCD的边长为2,沿对角线AC将三角形ADC折起,使平面ADC与平面ABC垂直,折叠后B、D两点的距离是( )
如图,已知正方形ABCD的边长为2,沿对角线AC将三角形ADC折起,使平面ADC与平面ABC垂直,折叠后B、D两点的距离是( )
