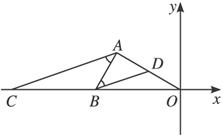
题目内容

已知
OA
=
a
，
CB
=
b
点G是△OAB的重心，过点G的直线PQ与OA，OB分别交于P，Q两点．
（1）用
a
，
b
表示
OG
；
（2）若
OP
=m
a
，
OQ
=n
b
试问
1
m
+
1
n
是否为定值，证明你的结论．
分析：（1）先设D为AB的中点，则
OD
=
1
2
(
a
+
b
)，根据重心的性质求出向量
OG
，
（2）结合（1）中结论，然后根据P、Q、G共线建立等式关系，根据向量的性质可得到方程组，即可求出所求．
解答：解：（1）解：设D为AB的中点
则
OD
=
1
2
(
a
+
b
)，
OG
=
2
3
OD
=
1
3
(
a
+
b
)
∴
OG
=
1
3
(
a
+
b
)；
（2）
PG
=(
1
3
-m)
a
+
1
3
b
，
GQ
=-
1
3
a
+(n-
1
3
)
b

设
PG
=λ
GQ
得：
（
1
3
-m+
1λ
3
）
a
=[（n-
1
3
）λ-
1
3
]
b

又
a
，
b
不共线，
故
1
3
-m+
1λ
3
=（n-
1
3
）λ-
1
3
=0，
故
1
m
+
1
n
=3是定值．
点评：本题主要考查了重心的性质，以及向量的加减数乘的运算和几何意义，属于基础题．
练习册系列答案
相关题目
已知
OA
=
a
，
OB
=
b
，C为线段AB上距A较近的一个三等分点，D为线段CB上距C较近的一个三等分点，则用
a
，
b
表示
OD
的表达式为（　　）
A、
1
9
(4
a
+5
b
)
B、
1
16
(9
a
+7
b
)
C、
1
3
(2
a
+
b
)
D、
1
4
(3
a
+
b
)
已知
OA
=(-1，1)，
OB
=(0，-1)，
OC
=(1，m)(m∈R)．
（1）若A，B，C三点共线，求实数m的值；
（2）证明：对任意实数m，恒有 
CA
•
CB
≥1成立．
如图，已知点A在第二象限，AB⊥OA交x轴于B，点C在OB延长线上，且CB=BO，若∠CAB=45°，求以OA为终边的角α的正弦和余弦值.

已知
OA
=
a
，
OB
=
b
，C为线段AB上距A较近的一个三等分点，D为线段CB上距C较近的一个三等分点，则用
a
，
b
表示
OD
的表达式为（　　）
A．
1
9
(4
a
+5
b
)		B．
1
16
(9
a
+7
b
)		C．
1
3
(2
a
+
b
)		D．
1
4
(3
a
+
b
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网