题目内容
已知函数f(x)=x-
-3lnax,其中a≠0.
(1)讨论f(x)的单调性;
(2)假定函数f(x)在点P处的切线为l,如果l与函数f(x)的图象除P外再无其它公共点,则称l是f(x)的一条“单纯切线”,我们称P为“单纯切点”.设f(x)的“单纯切点”P为(x0,f(x0)),当a>0时,求x0的取值范围.
| 2 |
| x |
(1)讨论f(x)的单调性;
(2)假定函数f(x)在点P处的切线为l,如果l与函数f(x)的图象除P外再无其它公共点,则称l是f(x)的一条“单纯切线”,我们称P为“单纯切点”.设f(x)的“单纯切点”P为(x0,f(x0)),当a>0时,求x0的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)利用导数与函数单调性的关系,分类讨论得出单调区间;
(2)由f′(x)=
得f′(x0)=
,过(x0,f(x0))的切线是l:y=f'(x0)(x-x0)+f(x0).构造g(x)=f(x)-L(x)=f(x)-[f′(x0)(x-x0)+f(x0)],故g′(x)=f′(x)-f′(x0)=
-
=
.由 g(x0)=0,依题意,x0应是g(x)的唯一零点.故对x0分类讨论得出结论.
(2)由f′(x)=
| (x-1)(x-2) |
| x2 |
| (x0-1)(x0-2) |
| x02 |
| (x-1)(x-2) |
| x2 |
| (x0-1)(x0-2) |
| x02 |
| (3x0-2)x2-3x02x+2x02 |
| x2x02 |
解答:
解:(1)当a>0时,f(x)的定义域是(0,+∞),由f′(x)=1+
-
=
,…(1分)
令f'(x)>0得x>2或x<1,f'(x)<0得1<x<2,所以增区间是(0,1)、(2,+∞),减区间是(1,2). …(4分)
当a<0时,则x<0,f′(x)=1+
-
=
>0,所f(x)在(-∞,0)上为增函数. …(6分)
(2)由f′(x)=
得f′(x0)=
,过(x0,f(x0))的切线是l:y=f'(x0)(x-x0)+f(x0). …(7分)
构造g(x)=f(x)-L(x)=f(x)-[f′(x0)(x-x0)+f(x0)],…(8分)
显然 g(x0)=0,依题意,x0应是g(x)的唯一零点.g′(x)=f′(x)-f′(x0)=
-
=
.
①如果x0=
,则g′(x)=
,由g′(x)=0⇒x=
,易看出g(x)在(0,
]为减函数,在[
,+∞)上为增函数,故x=
是唯一零点.…(9分)
②如果0<x0<
,则有g′(x)=
,由g′(x)=0得x=x0,
(x=
<0舍去),g(x)在(0,x0)为减函数,在(x0,+∞)上为增函数,故x=x0是唯一零点. …(10分)
③如果x0>
,则由g′(x)=
=0得x=x0或x=
.
当
<x0<
时,x0>
,g(x)在[
,x0]为减函数,有g(
)>g(x0)=0,
而x→0时g(x)→-∞,g(x)在(-∞,
)有零点,不合要求;
当x0>
时,x0<
,g(x)在[x0,
]为减函数,有g(
)<g(x0)=0,
同理得g(x)在(
,+∞)有零点,不合要求; …(12分)
当x0=
时,x0=
,则g′(x)=
≥0,所以g(x)在(0,+∞)为增函数,x=x0是唯一零点.
综上所述,x0的取值范围是(0,
]∪{
}. …(13分)
| 2 |
| x2 |
| 3 |
| x |
| (x-1)(x-2) |
| x2 |
令f'(x)>0得x>2或x<1,f'(x)<0得1<x<2,所以增区间是(0,1)、(2,+∞),减区间是(1,2). …(4分)
当a<0时,则x<0,f′(x)=1+
| 2 |
| x2 |
| 3 |
| x |
| (x-1)(x-2) |
| x2 |
(2)由f′(x)=
| (x-1)(x-2) |
| x2 |
| (x0-1)(x0-2) |
| x02 |
构造g(x)=f(x)-L(x)=f(x)-[f′(x0)(x-x0)+f(x0)],…(8分)
显然 g(x0)=0,依题意,x0应是g(x)的唯一零点.g′(x)=f′(x)-f′(x0)=
| (x-1)(x-2) |
| x2 |
| (x0-1)(x0-2) |
| x02 |
| (3x0-2)x2-3x02x+2x02 |
| x2x02 |
①如果x0=
| 2 |
| 3 |
| -3x+2 |
| x2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
②如果0<x0<
| 2 |
| 3 |
(3x0-2)(x-x0)(x-
| ||
| x2x02 |
(x=
| 2x0 |
| 3x0-2 |
③如果x0>
| 2 |
| 3 |
(3x0-2)(x-x0)(x-
| ||
| x2x02 |
| 2x0 |
| 3x0-2 |
当
| 2 |
| 3 |
| 4 |
| 3 |
| 2x0 |
| 3x0-2 |
| 2x0 |
| 3x0-2 |
| 2x0 |
| 3x0-2 |
而x→0时g(x)→-∞,g(x)在(-∞,
| 2x0 |
| 3x0-2 |
当x0>
| 4 |
| 3 |
| 2x0 |
| 3x0-2 |
| 2x0 |
| 3x0-2 |
| 2x0 |
| 3x0-2 |
同理得g(x)在(
| 2x0 |
| 3x0-2 |
当x0=
| 4 |
| 3 |
| 2x0 |
| 3x0-2 |
| (3x0-2)(x-x0)2 |
| x2x02 |
综上所述,x0的取值范围是(0,
| 2 |
| 3 |
| 4 |
| 3 |
点评:考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值以及函数的零点问题;
考查分类讨论思想,知识的转化与划归思想等.
考查分类讨论思想,知识的转化与划归思想等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若cos2t=-
cosxdx,其中t∈(0,π),则t=( )
| ∫ | t 0 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
已知命题P:函数f(x)=
+lg(3-x)的定义域为(2,3),命题Q:已知
,
为非零向量,则“函数f(x)=(
x+
)2为偶函数”是“
⊥
”的充分但不必要条件.则下列命题为真命题的有( )
| 3x | ||
|
| a |
| b |
| a |
| b |
| a |
| b |
| A、P∧Q |
| B、P∧(¬Q) |
| C、(¬P)∧Q |
| D、(¬P)∨Q |
如图是甲,乙两名同学5次综合测评成绩的茎叶图,下列四个结论中,正确的是( )
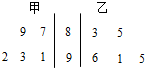

| A、甲成绩的极差大于乙成绩的极差 |
| B、甲成绩的中位数小于乙成绩的中位数 |
| C、甲成绩的平均值等于乙成绩的平均值 |
| D、甲成绩的标准差小于乙成绩的标准差 |
已知函数y=f(x)是定义在R上的奇函数,且f′(x)-f(x)>0(其中f′(x)是f(x)的导函数)恒成立.若a=
,b=
,c=-ef(1),则a,b,c的大小关( )
| f(ln3) |
| 3 |
| f(ln2) |
| 2 |
| A、a>b>c |
| B、c>a>b |
| C、c>b>a |
| D、a>c>b |
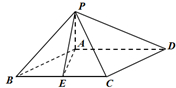 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,又PA⊥底面ABCD,AB=2PA,E为BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,又PA⊥底面ABCD,AB=2PA,E为BC的中点.