Question

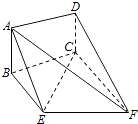
【题目】如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．
（Ⅰ） 证明：PA⊥BD；
（Ⅱ） 设PD=AD=1，求直线PC与平面ABCD所成角的正切值．

Answer 1

【答案】证明：（Ⅰ）在△ABD中，∠DAB=60°，AB=2AD，
由余弦定理可得：BD2=AB2+AD2﹣2ABADcos∠DAB，
∴BD2=5AD2﹣2AD2=3AD2 ， 则AB2=AD2+BD2 ， 即BD⊥AD．
又PD⊥平面ABCD，∴PD⊥BD．
∵PD∩AD=D，∴BD⊥平面PAD，则PA⊥BD；
（Ⅱ）解：∵PD⊥平面ABCD，∴∠PCD为PC与平面ABCD所称的角．
在Rt△BAD中，AD=1，∠DAB=60°，
∴AB=2，则DC=2，
∴tan∠PCD= ．

【解析】（Ⅰ）在△ABD中，由已知结合余弦定理可得BD2=3AD2 ， 进一步得到AB2=AD2+BD2 ， 可得BD⊥AD．再由PD⊥平面ABCD，可得PD⊥BD．由线面垂直的判定可得
BD⊥平面PAD，则PA⊥BD；（Ⅱ）由PD⊥平面ABCD，知∠PCD为PC与平面ABCD所称的角．在Rt△BAD中，求解直角三角形得AB=2，则DC=2，则tan∠PCD可求．
【考点精析】通过灵活运用直线与平面垂直的性质和空间角的异面直线所成的角，掌握垂直于同一个平面的两条直线平行；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则即可以解答此题．