Question

【题目】已知x，y满足约束条件 ，当目标函数z=ax+by（a＞0，b＞0）在该约束条件下取到最小值2 时，a2+b2的最小值为（ ）
A.5
B.4
C.
D.2

Answer 1

【答案】B
【解析】解：由约束条件 作可行域如图，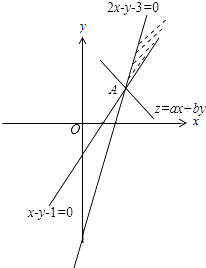
联立 ，解得：A（2，1）．
化目标函数为直线方程得： （b＞0）．
由图可知，当直线 过A点时，直线在y轴上的截距最小，z最小．
∴2a+b=2 ．
即2a+b﹣2 =0．
则a2+b2的最小值为 ．
故选：B．
由约束条件正常可行域，然后求出使目标函数取得最小值的点的坐标，代入目标函数得到2a+b﹣2 =0．a2+b2的几何意义为坐标原点到直线2a+b﹣2 =0的距离的平方，然后由点到直线的距离公式得答案．