题目内容
已知函数
上一点P（1，－2），过点P作直线l，（Ⅰ）求使直线l和y=f（x）相切且以P为切点的直线方程；（Ⅱ）求使直线l和y=f（x）相切且切点异于P的直线方程y=g（x）；（Ⅲ）在（Ⅱ）的条件下，求
上单调时，t的取值范围．
(Ⅰ) 
(Ⅱ) 
（Ⅲ）
解析:
:（Ⅰ）由
过点P且以P（1，－2）为切点的直线的斜率
，
所求直线方程：
(3分)
（Ⅱ）设过P（1，－2）的直线l与
切于另一点
知：
即：
或
故所求直线的斜率为：
即
(8分)
（Ⅲ）由（Ⅱ）可知
则
在
上单调递增， (11分)
在
得
为两极值点，在
时，
上单调递增，
即
(14分)
练习册系列答案
相关题目
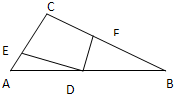（1）如图，D是Rt△ABC的斜边AB上的中点，E和F分别在边AC和BC上，且ED⊥FD，求证：EF2=AE2+BF2（EF2表示线段EF长度的平方）（尝试用向量法证明）
上一点P（1，－2），过点P作直线l，（Ⅰ）求使直线l和y=f（x）相切且以P为切点的直线方程；（Ⅱ）求使直线l和y=f（x）相切且切点异于P的直线方程y=g（x）；（Ⅲ）在（Ⅱ）的条件下，求
上单调时，t的取值范围．