题目内容
已知数列{an}满足:a1=1,an>0, =1(n∈N*),那么使an<5成立的n的最大值为 ( ).
=1(n∈N*),那么使an<5成立的n的最大值为 ( ).
 =1(n∈N*),那么使an<5成立的n的最大值为 ( ).
=1(n∈N*),那么使an<5成立的n的最大值为 ( ).| A.4 | B.5 | C.24 | D.25 |
C
由a1=1,an>0, =1(n∈N*),
=1(n∈N*),
∴{ }是以1为首项,公差为1的等差数列,
}是以1为首项,公差为1的等差数列,
∴ =n,即an=
=n,即an= ,要使an<5,则n<25.
,要使an<5,则n<25.
 =1(n∈N*),
=1(n∈N*),∴{
 }是以1为首项,公差为1的等差数列,
}是以1为首项,公差为1的等差数列,∴
 =n,即an=
=n,即an= ,要使an<5,则n<25.
,要使an<5,则n<25.
练习册系列答案
相关题目
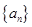 满足
满足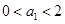 ,
,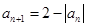 ,
,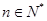 .
.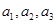 成等比数列,求
成等比数列,求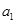 的值;
的值; 是公差不为零的等差数列,并且
是公差不为零的等差数列,并且 是等比数列
是等比数列 的相邻三项,若
的相邻三项,若 ,则
,则 等于( )
等于( )



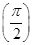 =0.
=0.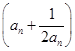 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.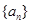 的公差
的公差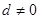 ,
,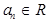 ,前
,前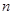 项和为
项和为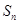 ,则对正整数
,则对正整数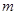 ,下列四个结论中:
,下列四个结论中: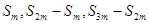 成等差数列,也可能成等比数列;
成等差数列,也可能成等比数列;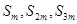 可能成等比数列,但不可能成等差数列;
可能成等比数列,但不可能成等差数列;