题目内容
如图,平面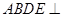 平面
平面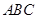 ,
,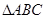 是等腰直角三角形,
是等腰直角三角形,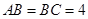 ,四边形
,四边形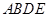 是直角梯形,
是直角梯形,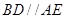 ,
,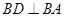 ,
,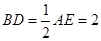 ,点
,点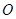 、
、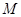 分别为
分别为 、
、 的中点.
的中点.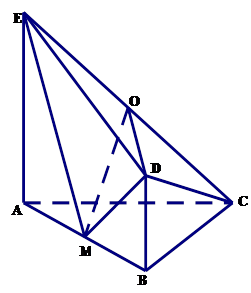
(1)求证: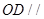 平面
平面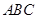 ;
;
(2)求直线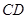 和平面
和平面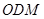 所成角的正弦值;
所成角的正弦值;
(3)能否在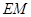 上找到一点
上找到一点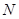 ,使得
,使得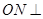 平面
平面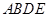 ?若能,请指出点
?若能,请指出点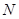 的位置,并加以证明;若不能,请说明理由 .
的位置,并加以证明;若不能,请说明理由 .
(1)见解析;(2) ;(3)见解析.
;(3)见解析.
解析试题分析:(1)先建立空间直角坐标系,利用法向量证明OD//平面ABC,说明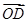 和平面ABC的法向量
和平面ABC的法向量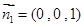 垂直即可;(2)设直线CD与平面ODM所成角为θ,求出平面ODM法向量
垂直即可;(2)设直线CD与平面ODM所成角为θ,求出平面ODM法向量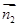 ,则
,则 ;(3)设EM上一点N满足,
;(3)设EM上一点N满足,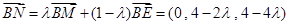 平面ABDE法向量
平面ABDE法向量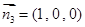 ,
,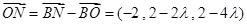 不存在
不存在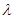 使
使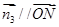 ∴ 不存在满足题意的点N.
∴ 不存在满足题意的点N.
试题解析:以B为原点,BC为x轴,BA为y轴,BD为z轴,建立空间直角坐标系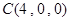 ,
,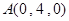 ,
,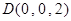 ,
,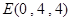 ,
,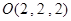 ,
,
(1)平面ABC的法向量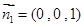 ,
,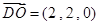 ,
,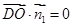
∴OD//平面ABC
(2)设平面ODM法向量为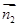 ,直线CD与平面ODM所成角为θ
,直线CD与平面ODM所成角为θ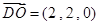 ,
,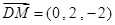 ,∴
,∴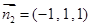 ,
,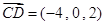
∴ .
.
(3)设EM上一点N满足,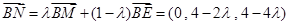
平面ABDE法向量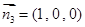 ,
,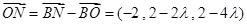
不存在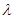 使
使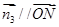 ∴不存在满足题意的点N.
∴不存在满足题意的点N.
(传统方法参照给分)
考点:空间向量的运算、空间向量解决立体几何中的证明和计算.

练习册系列答案
相关题目

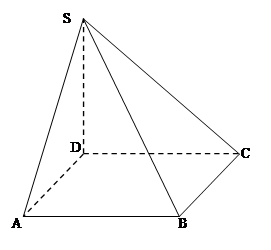
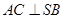 ;(2)求直线
;(2)求直线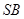 与平面
与平面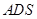 所成角的正弦值.
所成角的正弦值.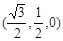 ,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.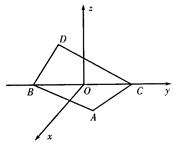
 的值.
的值.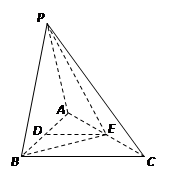
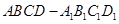 中,底面
中,底面 为平行四边形,且
为平行四边形,且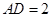 ,
,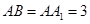 ,
,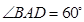 ,
,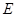 为
为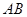 的中点.
的中点.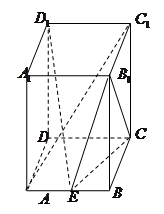
 ∥平面
∥平面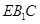 ;
;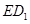 与平面
与平面 中,底面
中,底面 为矩形,
为矩形,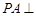 平面
平面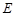 在线段
在线段 上,
上,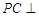 平面
平面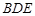 .
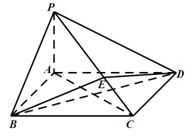
.
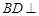 平面
平面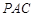 ;
; ,
, ,求二面角
,求二面角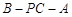 的正切值.
的正切值.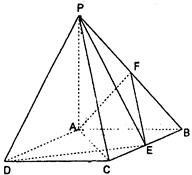
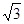 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.

 的面积。
的面积。