题目内容

如图所示,已知椭圆=1(a＞b＞0)内一点A,F1为左焦点,在椭圆上求一点P,使|PF1|+|PA|取得最值.

解析:根据椭圆的定义|PF1|+|PF2|=2a,

∴|PF1|=2a-|PF2|.

∴|PF1|+|PA|=2a+(|PA|-|PF2|).

在△PAF2中,|PA|-|PF2|≤|AF2|.

当且仅当点P在AF2的延长线上时|PA|-|PF2|取得最大值|AF2|.

此时|PF1|+|PA|最大为=2a+|AF2|.

又△PAF2中,|PF2|-|PA|≤|AF2|,

当且仅当点P在F2A的延长线上时,|PA|-|PF2|取得最小值-|AF2|.

此时|PF1|+|PA|最小为2a-|AF2|.

练习册系列答案
相关题目
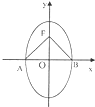精英家教网如图所示，已知椭圆的方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，A为椭圆的左顶点，B，C在椭圆上，若四边形OABC为平行四边形，且∠OAB=45°，则椭圆的离心率等于（　　）
A、
2
2
B、
3
3
C、
6
3
D、
2
2
3
（文）如图所示：已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，F1、F2为其左、右焦点，A为右顶点，过F1的直线l与椭圆相交于P、Q两点，且有
1
|PF1|
+
1
|QF|
=2．
（1）求椭圆长半轴长a的取值范围；
（2）若
AP
•
AQ
=a2且a∈(
4
3
，
9
5
)，求直线l的斜率的取值范围．
精英家教网如图所示，已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的3倍且经过点M（3，1）．平行于OM的直线l在y轴上的截距为m（m≠0），且交椭圆于A，B两不同点．
（1）求椭圆的方程；
（2）求m的取值范围；
如图所示，已知椭圆C：x2+
y2
a2
=1（a＞1）的离心率为e，点F为其下焦点，点A为其上顶点，过F的直线l：y=mx-c（其中c=
a2-1
与椭圆C相交于P，Q两点，且满足
AP
•
AQ
=
a2(a+c)2-1
2-c2
．
（1）试用a表示m2；
（2）求e的最大值；
（3）若e∈（
1
3
，
1
2
），求m的取值范围．
精英家教网如图所示：已知椭圆方程为
y2
a2
+
x2
b2
=1(a＞b＞0)，A，B是椭圆与斜轴的两个交点，F是椭圆的焦点，且△ABF为直角三角形．
（1）求椭圆离心率；
（2）若椭圆的短轴长为2，过F的直线与椭圆相交的弦长为
3
2
2
，试求弦所在直线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网