题目内容
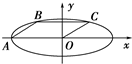 如图所示,已知椭圆的方程为
如图所示,已知椭圆的方程为| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由图形知|BC|=a,且BC∥OA由椭圆的对称性知,B,C两点关于y轴对称,由此可以求出两点的坐标,再连接OC,有∠OAB=45°及平行的性质,椭圆的对称性,令椭圆的右端点为M,则有∠COM=∠CMO=∠OAB=45°由此可得CO垂直于MC,由此垂直关系建立方程即可求得离心率的值.
解答:解:令椭圆的右端点为M,连接CM,由题意四边形OABC为平行四边形,且∠OAB=45°,B,C在椭圆上,可得∠COM=∠CMO=∠OAB=45°,则有∠OCM=90°,故可得kOC×kCM=-1
又四边形OABC为平行四边形,B,C在椭圆上,由图形知|BC|=a,且BC∥OA由椭圆的对称性知,B,C两点关于y轴对称,故C的横坐标为
,代入椭圆的方程得
+
=1,解得y=±
b,
由图形知C(
,
b),故有kOC=
,kCM=
,所以有
×
=-1解得a2=3b2,故可得c2=2b2,所以e2=
,得e=
故选C
又四边形OABC为平行四边形,B,C在椭圆上,由图形知|BC|=a,且BC∥OA由椭圆的对称性知,B,C两点关于y轴对称,故C的横坐标为
| a |
| 2 |
(
| ||
| a2 |
| y2 |
| b2 |
| ||
| 2 |
由图形知C(
| a |
| 2 |
| ||
| 2 |
| ||||
|
| ||||
-
|
| ||||
|
| ||||
-
|
| 2 |
| 3 |
| ||
| 3 |
故选C
点评:本题考查椭圆的简单性质,求解本题的关键是根据椭圆的对称性得出点C的坐标以及图形中的垂直关系,求出点C的坐标是为了表示出斜率,求出垂直关系是为了利用斜率的乘积为-1建立方程,然后再根据求离心率的公式求出离心率即可.本题比较抽象,方法单一,入手较难,运算量不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
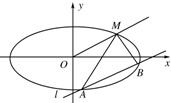 如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1).平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点.
如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1).平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点.
 ,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
 B.
B. C.
C. D.
D.
 如图所示,已知椭圆的方程为
如图所示,已知椭圆的方程为 ,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )


