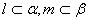题目内容
 (文)如图所示:已知椭圆C:
(文)如图所示:已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| |PF1| |
| 1 |
| |QF| |
(1)求椭圆长半轴长a的取值范围;
(2)若
| AP |
| AQ |
| 4 |
| 3 |
| 9 |
| 5 |
分析:(1)分类讨论:若直线l与x轴垂直,容易得到
+
=
;若直线l与x轴不垂直,则如图分别过点P、Q,作左准线的垂线,垂足分别为P1,Q1,利用△PF1F∽△PQS得出比例式,从而有:
=2⇒a=b2,所以a2>a>0,得到a的取值范围;
(2)设直线l的方程为x=my-c代入椭圆方程,消去x得到关于y的一元二次方程,再结合根系数的关系利用向量数量积公式即可求得m与a的关系式,再利用m2 的范围,从而求直线l的斜率的取值范围.
| 1 |
| |PF1| |
| 1 |
| |QF1| |
| 2a |
| b2 |
| 2a |
| b2 |
(2)设直线l的方程为x=my-c代入椭圆方程,消去x得到关于y的一元二次方程,再结合根系数的关系利用向量数量积公式即可求得m与a的关系式,再利用m2 的范围,从而求直线l的斜率的取值范围.
解答:解: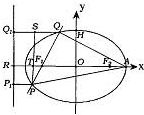 (文)(1)若直线l与x轴垂直,容易得到
(文)(1)若直线l与x轴垂直,容易得到
+
=
若直线l与x轴不垂直,则如图分别过点P、Q
作左准线的垂线,垂足分别为P1,Q1,
得到:|PP1|=
,QQ1=
,
∵△PF1F∽△PQS
∴
=
⇒b2(|PF1|+|QF1|)-a|PF1|2-a|PF1|•|QF1|=a|PF1|•|QF1|-a|PF1|2
所以
+
=
…(4分)
从而有:
=2⇒a=b2,所以a2>a>0得到:a>1; …(6分)
(2)设直线l的方程为x=my-c代入椭圆方程得到:(a2+b2m2)y2-2b2cmy-b4=0,
设,则有:y1+y2=
,y1y2=
,
所以x1+x2=m(y1+y2)-2c=
,
x1•x2=(my1-c)•(my2-c)=m2y1y2-mc(y1+y2)+c2=
,…(9分)
得到
•
=(x1-a)(x2-a)+y1y2=x1x2-a(x1+x2)+a2+y1y2
=
-
=a2⇒
=a2
⇒m2=
=2
+a-1-
,…(12分)
当a∈(
,
)时,m2随着a增大而增大,所以
<m2<
,
所以斜率k满足:
<k2<
,
所以斜率的取值范围是 [-
,-
]∪[
,
]…(14分)
 (文)(1)若直线l与x轴垂直,容易得到
(文)(1)若直线l与x轴垂直,容易得到| 1 |
| |PF1| |
| 1 |
| |QF1| |
| 2a |
| b2 |
若直线l与x轴不垂直,则如图分别过点P、Q
作左准线的垂线,垂足分别为P1,Q1,
得到:|PP1|=
| a|F1P| |
| c |
| a|F1Q| |
| c |
∵△PF1F∽△PQS
∴
| ||||
|
| |PF1| |
| |PF1|+|QF1| |
所以
| 1 |
| |PF1| |
| 1 |
| |QF1| |
| 2a |
| b2 |
从而有:
| 2a |
| b2 |
(2)设直线l的方程为x=my-c代入椭圆方程得到:(a2+b2m2)y2-2b2cmy-b4=0,
设,则有:y1+y2=
| 2b2m |
| a2+b2m2 |
| -4 |
| a2+b2m2 |
所以x1+x2=m(y1+y2)-2c=
| -2a2c |
| a2+b2m2 |
x1•x2=(my1-c)•(my2-c)=m2y1y2-mc(y1+y2)+c2=
| a2(-b2m2+c2) |
| a2+b2m2 |
得到
| AP |
| AQ |
=
| a2(a+c)2 |
| a2+b2m2 |
| b4 |
| a2+b2m2 |
| a2(a+c)2-a2 |
| a2+b2m2 |
⇒m2=
| 2ac+c2-1 |
| a |
| a2-a |
| 1 |
| a |
当a∈(
| 4 |
| 3 |
| 9 |
| 5 |
| 11 |
| 12 |
| 119 |
| 45 |
所以斜率k满足:
| 45 |
| 119 |
| 12 |
| 11 |
所以斜率的取值范围是 [-
2
| ||
| 11 |
3
| ||
| 119 |
3
| ||
| 119 |
2
| ||
| 11 |
点评:本小题主要考查直线的斜率、椭圆的简单性质、平面向量数量积的运算等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

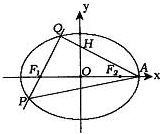 (文)如图所示:已知椭圆C:
(文)如图所示:已知椭圆C: ,F1、F2为其左、右焦点,A为右顶点,过F1的直线l与椭圆相交于P、Q两点,且有
,F1、F2为其左、右焦点,A为右顶点,过F1的直线l与椭圆相交于P、Q两点,且有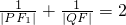 .
.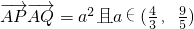 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围. ,F1、F2为其左、右焦点,A为右顶点,过F1的直线l与椭圆相交于P、Q两点,且有
,F1、F2为其左、右焦点,A为右顶点,过F1的直线l与椭圆相交于P、Q两点,且有 .
. ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.