题目内容
若有一扇形的周长为60cm，那么扇形的最大面积为（ ）
| A、500cm2 |
| B、60cm2 |
| C、225cm2 |
| D、30cm2 |
考点：扇形面积公式
专题：三角函数的求值
分析：设扇形的半径为r，弧长为l，利用周长关系，表示出扇形的面积，利用二次函数求出面积的最大值，以及圆心角的大小．
解答：
解：设扇形的半径为r，弧长为l，则
l+2r=60，即l=60-2r（0＜r＜30）．
扇形的面积S=
lr，将上式代入，
得S=
（60-2r）r=-r2+30r
=-（r-15）2+225，
所以当且仅当r=15时，S有最大值225．
扇形的面积的最大值为225cm2．
故选：C．
l+2r=60，即l=60-2r（0＜r＜30）．
扇形的面积S=
| 1 |
| 2 |
得S=
| 1 |
| 2 |
=-（r-15）2+225，
所以当且仅当r=15时，S有最大值225．
扇形的面积的最大值为225cm2．
故选：C．
点评：本题是基础题，考查扇形的周长，半径圆心角，面积之间的关系，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若角α、β的终边关于y轴对称，则下列等式成立的是（ ）
| A、sinα=sinβ |
| B、cosα=cosβ |
| C、tanα=tanβ |
| D、cotα=cotβ |
以下是解决数学问题的思维过程的流程图：
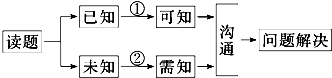
在此流程图中，①②两条流程线与“推理与证明”中的思维方法匹配正确的是（ ）
在此流程图中，①②两条流程线与“推理与证明”中的思维方法匹配正确的是（ ）
| A、①-综合法，②-分析法 |
| B、①-分析法，②-综合法 |
| C、①-综合法，②-反证法 |
| D、①-分析法，②-反证法 |
已知曲线y=2x2上一点A（2，8），则A处的切线斜率为（ ）
| A、4 | B、16 | C、8 | D、2 |
两个变量y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R2如下，其中拟合效果最好的模型是（ ）
| A、模型1的相关指数R2为0.98 |
| B、模型2的相关指数R2为0.86 |
| C、模型3的相关指数R2为0.68 |
| D、模型4的相关指数R2为0.58 |
若函数f（x）=
x3+atanx-bx+
，且f（1）=-1，则f（-1）=（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
下列选项中叙述正确的是（ ）
| A、三角形的内角是第一象限角或第二象限角 |
| B、小于90°的角一定是锐角 |
| C、锐角一定是第一象限的角 |
| D、终边相同的角一定相等 |