Question

已知三棱锥SABC，在三棱锥内任取一点P，使得V_P-ABC＜

1

2

V_S-ABC的概率是（　　）

• A、

  7

  8

• B、

  3

  4

• C、

  1

  2

• D、

  1

  4

Answer 1

考点：几何概型

专题：概率与统计

分析：取高线的中点，过该点作平行于底的平面，若V_P-ABC＜

1

2

V_S-ABC，则P点在平面EFG与底面ABC之间，所以概率为棱台与原棱锥体积之比，用相似比计算即可．

解答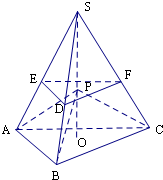： 解：作出S在底面△ABC的射影为O，
若V_P-ABC=

1

2

V_S-ABC，则高OP=

1

2

SO，
即此时P在三棱锥V_S-ABC的中垂面DEF上，
则V_P-ABC＜

1

2

V_S-ABC的点P位于在三棱锥V_S-ABC的中垂面DEF以下的棱台内，
则对应的概率P=1-（

1

2

）³=

7

8

，
故选：A．

点评：本题主要考查几何概型的概率计算，求出对应的体积关系是解决本题的关键，根据比例关系，得到面积之比是相似比的平方，体积之比是相似比的立方．