题目内容
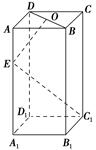
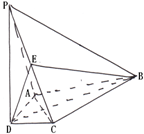
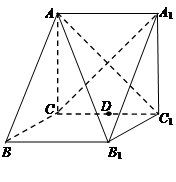
如图,四棱锥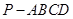 的底面
的底面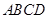 是正方形,棱
是正方形,棱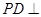 底面
底面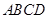 ,
,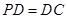 ,
,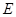 是
是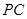 的中点.
的中点.
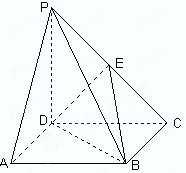
(1)证明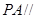 平面
平面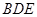 ;
;
(2)证明平面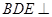 平面
平面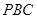 .
.
 的底面
的底面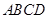 是正方形,棱
是正方形,棱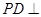 底面
底面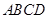 ,
,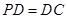 ,
,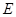 是
是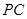 的中点.
的中点.
(1)证明
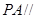 平面
平面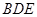 ;
;(2)证明平面
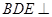 平面
平面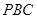 .
.(1)详见解析;(2)详见解析.
试题分析:(1)由
 推出
推出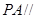 平面
平面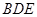 ;(2)由
;(2)由 ,
, 推出
推出 底面
底面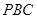 ,进而推出平面
,进而推出平面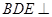 平面
平面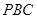 .
.试题解析:(1)连结
 ,设
,设 与
与 交于
交于 点,连结
点,连结 .
.∵底面ABCD是正方形,∴
 为
为 的中点,又
的中点,又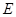 为
为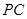 的中点,
的中点,∴
 , ∵
, ∵ 平面
平面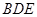 ,
, 平面
平面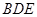 ,
,∴
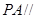 平面
平面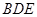 .
. (2)∵
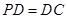 ,
,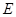 是
是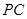 的中点, ∴
的中点, ∴ .
.∵
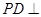 底面
底面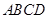 ,∴
,∴ .又由于
.又由于 ,
, ,故
,故 底面
底面 ,
,所以有
 .又由题意得
.又由题意得 ,故
,故
 .
.于是,由
 ,
, ,
, 可得
可得 底面
底面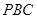 .
.故可得平面
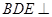 平面
平面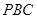 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
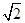 ,OE⊥EC1,求AA1的长.
,OE⊥EC1,求AA1的长.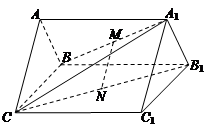
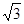 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小 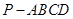 中,
中,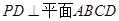 ,
,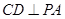 ,
, 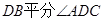 ,
,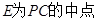 ,
,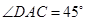 ,
,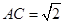 .
.
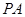 ∥
∥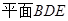 ;
;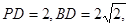 求四棱锥
求四棱锥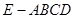 的体积
的体积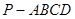 中,底面
中,底面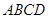 是矩形,
是矩形,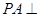 底面
底面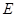 是
是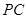 的中点,已知
的中点,已知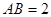 ,
,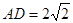 ,
,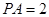 ,
,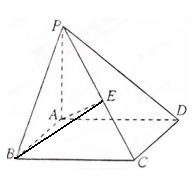
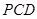 的面积;(II)三棱锥
的面积;(II)三棱锥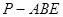 的体积
的体积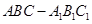 中,侧棱
中,侧棱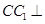 底面
底面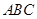 ,
,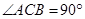 ,
,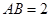 ,
,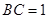 ,
,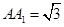 .
.
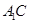
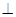 平面
平面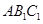 ;
;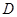 是棱
是棱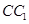 的中点,在棱
的中点,在棱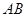 上是否存在一点
上是否存在一点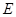 ,使
,使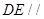 平面
平面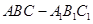 中,
中,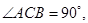
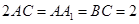 ,
,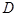 为
为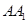 的中点
的中点
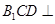 平面
平面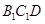 ;
;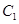 到平面
到平面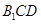 的距离.
的距离.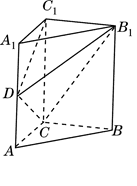
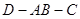 ,如图二,在二面角
,如图二,在二面角