题目内容
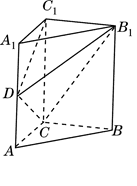
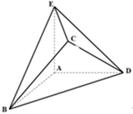
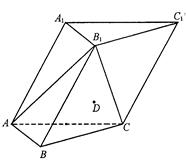
如图,在直三棱柱(即侧棱与底面垂直的三棱柱)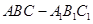 中,
中,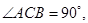
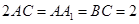 ,
,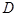 为
为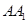 的中点
的中点
(I)求证:平面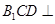 平面
平面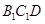 ;
;
(II)求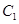 到平面
到平面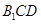 的距离.
的距离.
 中,
中,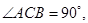
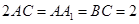 ,
, 为
为 的中点
的中点
(I)求证:平面
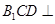 平面
平面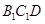 ;
;(II)求
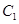 到平面
到平面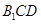 的距离.
的距离.
(I)略;(II) .
.
 .
.试题分析:(I)可以转化为证线面垂直(如转化为证明
 平面
平面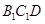 );(II)可利用等积法求点面距.设
);(II)可利用等积法求点面距.设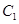 到平面
到平面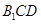 的距离为
的距离为 ,利用
,利用 ,列出关于
,列出关于 的方程
的方程 ,得
,得 ,进而可求得
,进而可求得 .
.试题解析:(I)证明:∵
 ,∴
,∴ .
. 
又由直三棱柱的性质知
 ,
, 
∴
 平面
平面 .
.∴
 , ①
, ①
由
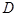 为
为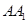 的中点,可知
的中点,可知 ,
,∴
 ,即
,即 , ②
, ②
又
 ③
③由①②③可知
 平面
平面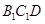 ,
, 
又
 平面
平面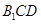 ,故平面
,故平面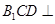 平面
平面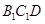 .
. 
(II)设
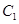 到平面
到平面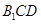 的距离为
的距离为 ,由(I)知CD⊥平面B1C1D,
,由(I)知CD⊥平面B1C1D,所以


而由
 可得
可得

又


所以



练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
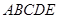 中,
中,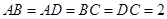 ,
,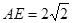 ,
,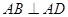 ,且
,且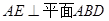 ,
,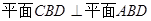 .
.
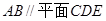 ;
;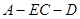 的余弦值.
的余弦值.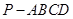 的底面
的底面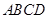 是正方形,棱
是正方形,棱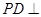 底面
底面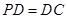 ,
,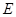 是
是 的中点.
的中点.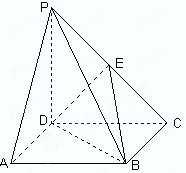
 平面
平面 ;
;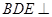 平面
平面 .
.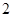 的三棱柱
的三棱柱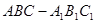 中,侧面
中,侧面 底面
底面 ,
, .
.
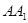 与平面
与平面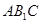 所成角的正弦值的大小;
所成角的正弦值的大小; 满足
满足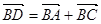 ,在直线
,在直线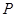 ,使
,使 ?若存在,请确定点
?若存在,请确定点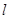 与平面
与平面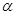 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题: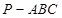 中,
中,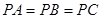 ,底面
,底面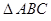 是正三角形,
是正三角形,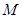 、
、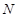 分别是侧棱
分别是侧棱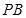 、
、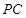 的中点.若平面
的中点.若平面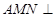 平面
平面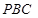 ,则平面
,则平面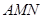 与平面
与平面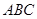 所成二面角(锐角)的余弦值等于( )
所成二面角(锐角)的余弦值等于( )




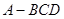 ,平面
,平面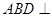 平面
平面 ,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC
,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC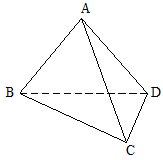
 的正切值.
的正切值. 中,已知
中,已知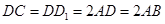 ,
,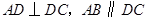 .
.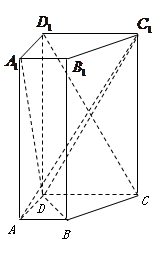
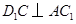 ;
;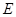 是
是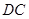 上一点,试确定
上一点,试确定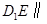 平面
平面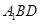 ,并说明理由.
,并说明理由.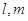 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,在下列条件中,能成为
是两个不同的平面,在下列条件中,能成为 的充分条件的是( )
的充分条件的是( ) ,
, 与
与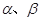 所成角相等
所成角相等 内的射影分别为
内的射影分别为 ,且
,且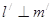
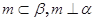
 ,
,