题目内容

15．在Rt△ABC中，∠A=30°，在斜边AB上取点M，则使|AM|＞|AC|的概率为$\frac{2-\sqrt{3}}{2}$．

分析 根据三角形的性质，求得三边的值，利用几何概型求得P．

解答 解：设|AM|＞|AC|的事件为A，
由三角的关系可知，在Rt△ABC中，∠A=30°则AB=2BC，AC=$\sqrt{3}$BC，
由几何概型可知P（A）=$\frac{2-\sqrt{3}}{2}$，
故答案为：$\frac{2-\sqrt{3}}{2}$．

点评 本题主要考察三角形三边的关系和几何概型，属于基础题．

练习册系列答案
相关题目
5．在平面四边形ACBD（图①）中，△ABC与△ABD均为直角三角形且有公共斜边AB，设AB=2，∠BAD=30°，∠BAC=45°，将△ABC沿AB折起，构成如图②所示的三棱锥C′-ABC．
（Ⅰ）当$C'D=\sqrt{2}$时，求证：平面C′AB⊥平面DAB；①②
（Ⅱ）当AC′⊥BD时，求三棱锥C′-ABD的高．
6．已知点A（-3，2），在直线y=-x点找一点B，在x轴上找一点C，使此三点构成三角形，则△ABC的周长的最小值为$\sqrt{26}$．
3．根据函数y=f（x）的图象，求：f（0），f（3），定义域D，值域M，最值，单调减区间．
10．已知实数x，y满足x2+y2+2x-2$\sqrt{3}$y=0，则x2+y2的最大值为16．
20．设向量$\overrightarrow{a}$=（2，-4），$\overrightarrow{b}$=（6，x），若|$\overrightarrow{a}+\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|，则x=（　　）
A．3B．-3C．12D．-12
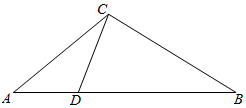7．如图，在△ABC中，点D在边AB上，AC=7，CD=5，BC=$\sqrt{31}$，BD=2AD
（1）求AD的长
（2）求△ABC的面积．
4．已知向量$\overrightarrow{m}$=（$\frac{3}{2}$，-sinx），$\overrightarrow{n}$=（1，sinx+$\sqrt{3}$cosx），x∈R，函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$．
（I）求f（x）的最小正周期及值域；
（2）已知△ABC中，角A、B、C的对边分别为a，b，c，若f（A）=0，a=$\sqrt{3}$，bc=2，求△ABC的周长．
5．2014年1月12日，中央党校举办第一期县委书记高级研修班培训，某省组织部从三个地区选派6名县委书记参加，每个地区派2名，培训后这6名县委书中有2名返回该省，但不在原地区担任县委书记（作岗位交流），且该2名县委书记不能在同一地区工作，其余4名县委书记组织部另有任用（可不做分工考虑），则不同的安排工作方式有（　　）
A．24种B．36种C．42种D．72种

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网