题目内容
设△ABC的内角A、B、C所对边的长分别为a、b、c，且cos2B+cosB+cos（A-C）=1．
（Ⅰ）证明：a、b、c成等比数列；
（Ⅱ）若a+c=b，cosB=
，求△ABC的面积．
（Ⅰ）证明：a、b、c成等比数列；
（Ⅱ）若a+c=b，cosB=
| 3 |
| 4 |
考点：余弦定理,等比关系的确定
专题：解三角形
分析：（Ⅰ）已知等式左边利用二倍角的余弦函数公式化简，再利用和差化积公式变形，根据正弦定理化简得到关系式，即可得证；
（Ⅱ）利用余弦定理列出关系式，把cosB的值代入并利用完全平方公式化简，整理求出ac的值，由cosB的值求出sinB的值，利用三角形面积公式计算即可得到结果．
（Ⅱ）利用余弦定理列出关系式，把cosB的值代入并利用完全平方公式化简，整理求出ac的值，由cosB的值求出sinB的值，利用三角形面积公式计算即可得到结果．
解答：
解：（Ⅰ）由已知得1-2sin2B+cosB+cos（A-C）=1，
cos（A-C）-cos（A+C）=2sin2B，即2sinAsinC=2sin2B，
由正弦定理知b2=ac，
∴a、b、c成等比数列；
（Ⅱ）由余弦定理知
=
=
=
，即ac=8，
∵sinB=
=
，
∴S△ABC=
acsinB=
×8×
=
．
cos（A-C）-cos（A+C）=2sin2B，即2sinAsinC=2sin2B，
由正弦定理知b2=ac，
∴a、b、c成等比数列；
（Ⅱ）由余弦定理知
| 3 |
| 4 |
| a2+c2-b2 |
| 2ac |
| (a+c)2-3ac |
| 2ac |
| 36-3ac |
| 2ac |
∵sinB=
| 1-cos2B |
| ||
| 4 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 7 |
点评：此题考查了正弦、余弦定理，以及三角形面积公式，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
二项式（3x-
）7展开式中，含x-3项的系数是（ ）
| 1 | |||
|
| A、-12 | B、18 |
| C、-20 | D、21 |
已知数列{an}是等比数列，其前n项和为Sn，若a4=4a3，S4=1，则S8=（ ）
| A、257 | B、16 |
| C、15 | D、256 |
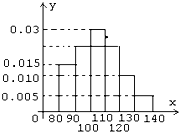某校高一某班共有64名学生，如图是该班某次数学考试成绩的频率分布直方图，根据该图可知，成绩在110-120间的同学大约有（ ）| A、10 | B、11 | C、13 | D、16 |
如图所示，椭圆函数y=
的定义域为（ ）
| ||
| lg(x+1) |
| A、（-1，3] |
| B、（-1，0）∪（0，3] |
| C、[-1，3] |
| D、[-1，0）∪（0，3] |