题目内容
20.已知a,b,c∈R+.(1)比较:$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$与$\frac{9}{2(a+b+c)}$的大小
(2)当$\frac{b}{a}$+$\frac{2c}{b}$+$\frac{4a}{c}$取最小值m时,求m+$\frac{b+c}{a}$的值.
分析 (1)利用基本不等式,即可得出结论;
(2)$\frac{b}{a}$+$\frac{2c}{b}$+$\frac{4a}{c}$≥3$\root{3}{\frac{b}{a}•\frac{2c}{b}•\frac{4a}{c}}$=6,当且仅当$\frac{b}{a}$=$\frac{2c}{b}$=$\frac{4a}{c}$=2时,取等号,即m=6,b=2a,c=2a,即可求m+$\frac{b+c}{a}$的值.
解答 解:(1)∵($\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$)[(a+b)+(b+c)+(c+a)]=3+$\frac{b+c}{a+b}+\frac{a+b}{b+c}$+$\frac{c+a}{a+b}+\frac{a+b}{c+a}$+$\frac{c+a}{b+c}+\frac{b+c}{c+a}$≥3+2+2+2=9,
∴$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$≥$\frac{9}{2(a+b+c)}$;
(2)$\frac{b}{a}$+$\frac{2c}{b}$+$\frac{4a}{c}$≥3$\root{3}{\frac{b}{a}•\frac{2c}{b}•\frac{4a}{c}}$=6,当且仅当$\frac{b}{a}$=$\frac{2c}{b}$=$\frac{4a}{c}$=2时,取等号,即m=6,b=2a,c=2a,
∴m+$\frac{b+c}{a}$=6+4=10.
点评 本题考查基本不等式的运用,考查学生的计算能力,正确运用基本不等式是关键.

练习册系列答案
相关题目
5.椭圆$\frac{{x}^{2}}{80}$+$\frac{{y}^{2}}{20}$=1上的点到直线x+2y-$\sqrt{10}$=0的最大距离是( )
| A. | 3 | B. | 5$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{10}$ |
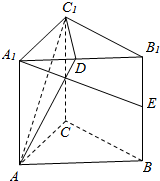 如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.
如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.