题目内容
某校高一(1)班共有42名学生,军训的时候,教官将这42人排成一列,自1起往下报数,报偶数的人出列;留下的人再重新报数,还是报偶数的人出列,…,这样下去,如果最后留下两个人,那么这两个人在第一次报数时报的数分别是 和 .
考点:进行简单的合情推理
专题:计算题,推理和证明
分析:根据第一次排除偶数,第二次排除奇数,第三次排除偶数…依次进行排除,即可得出结论
解答:
解:排除顺序如下:
第一次排除偶数号后剩下:
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41
第二次排除偶数号后剩下:
1 5 9 13 17 21 25 29 33 37 41
第三次排除偶数号后剩下:
1 9 17 25 33 41
第四次排除偶数号后剩下:
1 17 33
最后剩下:
1 33
故答案为:1,33
第一次排除偶数号后剩下:
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41
第二次排除偶数号后剩下:
1 5 9 13 17 21 25 29 33 37 41
第三次排除偶数号后剩下:
1 9 17 25 33 41
第四次排除偶数号后剩下:
1 17 33
最后剩下:
1 33
故答案为:1,33
点评:本题根据排除的顺序进行操作,比较基础.

练习册系列答案
相关题目
已知函数f(x)=sin(ωx+
)(x∈R,ω>0)与g(x)=cos(2x+φ)有相同的对称轴.为了得到h(x)=cos(ωx+
),只需将y=f(x)的图象( )
| π |
| 3 |
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
 已知某正三棱锥的三视图如图所示,其中正视图是边长为2的正三角形,则该正三棱锥的体积为
已知某正三棱锥的三视图如图所示,其中正视图是边长为2的正三角形,则该正三棱锥的体积为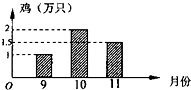 为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查.表格表示每个月所调查的养鸡场的个数,如图表示三个月中各养鸡场注射了疫苗的鸡的数量的平均数.根据图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为
为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查.表格表示每个月所调查的养鸡场的个数,如图表示三个月中各养鸡场注射了疫苗的鸡的数量的平均数.根据图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为 某市一公交线路某区间内共设置六个站点(如图所示),分别为A0,A1,A2,A3,A4,A5,现有甲、乙两人同时从A0站点上车,且他们中的每个人在站点Ai(i=1,2,3,4,5)下车是等可能的.则甲、乙两人不在同一站点下车的概率为( )
某市一公交线路某区间内共设置六个站点(如图所示),分别为A0,A1,A2,A3,A4,A5,现有甲、乙两人同时从A0站点上车,且他们中的每个人在站点Ai(i=1,2,3,4,5)下车是等可能的.则甲、乙两人不在同一站点下车的概率为( )