题目内容
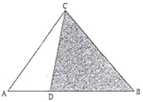 如图,在△ABC中,D是AB边上的点,且AD=
如图,在△ABC中,D是AB边上的点,且AD=| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:本题满足几何概型的条件,只要分别求出△ABC和阴影部分的面积,由几何概型的公式解答.
解答:
解:由题意,设△ABC的高为h,则△ABC的面积为
AB•h,阴影部分的面积为
×
AB•h,
由几何概型的公式可得随机丢一粒豆子在△ABC内,则它落在阴影部分的概率是
=
;
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
由几何概型的公式可得随机丢一粒豆子在△ABC内,则它落在阴影部分的概率是
| ||||
|
| 2 |
| 3 |
故选D.
点评:本题考查了几何概型的公式的运用;关键是明确概率模型的特点,正确选择测度,利用公式解答.

练习册系列答案
相关题目
若sinθ+cosθ=
,则tan(θ+
)的值是( )
| 2 |
| π |
| 3 |
| A、1 | ||
B、-
| ||
C、-1+
| ||
D、-
|
已知等差数列{an}中,a1,a4025是函数f(x)=
x3-3x2+5x+1的两个极值点,则2a2013值为( )
| 1 |
| 3 |
| A、32 | B、16 | C、8 | D、4 |
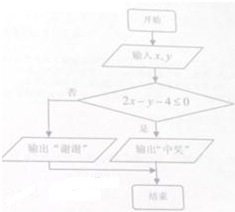 某市中学生田径运动会总分获得冠、亚、季军的代表队人数如图表中所示,大会组委会为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动,并用分层抽样方法从三个代表队中抽取16人在前排就座,其中亚军队有5人.
某市中学生田径运动会总分获得冠、亚、季军的代表队人数如图表中所示,大会组委会为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动,并用分层抽样方法从三个代表队中抽取16人在前排就座,其中亚军队有5人.