题目内容
△ABC中,B=120°,AC=3,AB=
,则△ABC的面积为
.
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
分析:利用余弦定理即可得出a,再利用三角形的面积计算公式即可得出.
解答:解:由余弦定理可得:AC2=BC2+AB2-2BC•AB•cosB,∴32=a2+(
)2-2
acos120°.
化为a2+
a-6=0,又a>0,解得a=
.
∴S△ABC=
acsinB=
×
×
×sin120°=
.
故答案为
.
| 3 |
| 3 |
化为a2+
| 3 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 4 |
| 3 |
故答案为
| 3 |
| 4 |
| 3 |
点评:本题考查了余弦定理和三角形的面积计算公式,属于基础题.

练习册系列答案
相关题目
在△ABC中,a=12,b=13,C=60°,此三角形的解的情况是( )
| A、无解 | B、一解 | C、二解 | D、不能确定 |
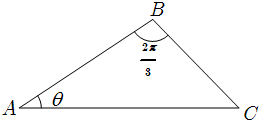 如图,△ABC中,
如图,△ABC中,