题目内容
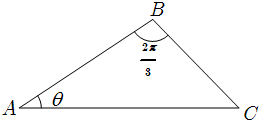 如图,△ABC中,∠B=
如图,△ABC中,∠B=| 2π |
| 3 |
(Ⅰ)若θ=
| π |
| 12 |
(Ⅱ)求f(θ)的解析式,并求f(θ)的单调区间.
分析:(Ⅰ)根据三角形的内角和定理,由∠A和∠B,求出∠C的度数,然后利用正弦定理,由AC,sinB和sinC的值,即可求出AB的长;
(Ⅱ)根据正弦定理,由AC,sinB和sinC,表示出AB,然后利用三角形的面积公式表示出三角形ABC的面积,把表示出的AB代入,利用两角差的正弦函数公式及特殊角的三角函数值,以及二倍角的正弦、余弦函数公式和两角和的正弦函数公式化为一个角的正弦函数,根据θ的范围,求出2θ+
的范围,根据正弦函数的单调区间,即可得到f(θ)的单调区间.
(Ⅱ)根据正弦定理,由AC,sinB和sinC,表示出AB,然后利用三角形的面积公式表示出三角形ABC的面积,把表示出的AB代入,利用两角差的正弦函数公式及特殊角的三角函数值,以及二倍角的正弦、余弦函数公式和两角和的正弦函数公式化为一个角的正弦函数,根据θ的范围,求出2θ+
| π |
| 6 |
解答:解:(Ⅰ)∠C=
-
=
,由正弦定理知:
=
∴AB=AC•
=
(Ⅱ)由正弦定理知:
=
,
∴AB=AC•
=
sin(
-θ),
∴f(θ)=S△ABC=
AB•AC•sinA=
sinθsin(
-θ),(0<θ<
)
∴f(θ)=
sinθsin(
-θ)=
sinθ(
cosθ-
sinθ)
=2sinθcosθ-
sin2θ=sin2θ-
(1-cos2θ)
=sin2θ+
cos2θ-
=
sin(2θ+
)-
,
又0<θ<
,
∴
<2θ+
<
,
由
<2θ+
≤
得0<θ≤
,由
<2θ+
<
得
<θ<
,
∴f(θ)在区间(0,
]上是增函数,在区间(
,
)上是减函数.
| π |
| 3 |
| π |
| 12 |
| π |
| 4 |
| AB |
| sinC |
| AC |
| sinB |
∴AB=AC•
sin
| ||
sin
|
2
| ||
| 3 |
(Ⅱ)由正弦定理知:
| AB |
| sinC |
| AC |
| sinB |
∴AB=AC•
sin(
| ||
sin
|
4
| ||
| 3 |
| π |
| 3 |
∴f(θ)=S△ABC=
| 1 |
| 2 |
4
| ||
| 3 |
| π |
| 3 |
| π |
| 3 |
∴f(θ)=
4
| ||
| 3 |
| π |
| 3 |
4
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
=2sinθcosθ-
2
| ||
| 3 |
| ||
| 3 |
=sin2θ+
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| π |
| 6 |
| ||
| 3 |
又0<θ<
| π |
| 3 |
∴
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
由
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∴f(θ)在区间(0,
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
点评:此题考查学生利用运用正弦定理及三角形的面积公式化简求值,熟练掌握三角函数的恒等变换,掌握正弦函数的单调区间,是一道中档题.

练习册系列答案
相关题目
 如图,
如图, 如图,△ABC中,
如图,△ABC中,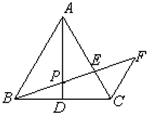 如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F, 已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.
已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.