题目内容
2.若圆x2+y2=b与直线x+y=b相切,则b的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\sqrt{2}$ |
分析 直线与圆相切,圆心到直线的距离为半径长,由点到直线间的距离公式即可求得b的值.
解答 解:由题意,圆与直线相切,可得圆心(0,0)到直线的距离等于半径$\sqrt{b}$,
由点到直线的距离公式可得:d=$\frac{|0×1+0×1-b|}{\sqrt{{1}^{2}+{1}^{2}}}=\sqrt{b}$,解得b=2或b=0(舍去)
故选择:C.
点评 解决此类问题,要对点到直线的距离公式熟练掌握,属于基本题型.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
12.若复数z=$\frac{3+2i}{1-i}$(i为虚数单位),则z的共轭复数$\overline{z}$为( )
| A. | $\frac{1}{2}$+$\frac{5}{2}$i | B. | $\frac{1}{2}$-$\frac{5}{2}$i | C. | $\frac{1}{2}$+2i | D. | $\frac{1}{2}$-2i |
14.已知i为虚数单位,则复数$\frac{3-4i}{1+i}$的虚部为( )
| A. | $-\frac{7}{2}$ | B. | $\frac{7}{2}$ | C. | $-\frac{7}{2}i$ | D. | $\frac{7}{2}i$ |
11.口袋中有编号分别为1、2、3的三个大小和形状相同的小球,从中任取2个,则取出的球的最大编号X的均值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
12.下列程序输出的结果是( )
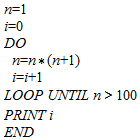
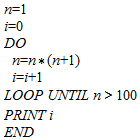
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下: