题目内容
14.在集合M={x|0<x≤5}中随机取一个元素,恰使函数$y={log_{\frac{1}{2}}}x$大于1的概率为( )| A. | $\frac{4}{5}$ | B. | $\frac{9}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{10}$ |
分析 解不等式$lo{g}_{\frac{1}{2}}x$≥1,可得0<x≤$\frac{1}{2}$,以长度为测度,即可求在集合M={x|0<x≤5}中随机取一个元素,恰使函数$y={log_{\frac{1}{2}}}x$大于1的概率.
解答 解:解不等式$lo{g}_{\frac{1}{2}}x$≥1,可得0<x≤$\frac{1}{2}$,
∴在集合M={x|0<x≤5}中随机取一个元素,恰使函数$y={log_{\frac{1}{2}}}x$大于1的概率为$\frac{\frac{1}{2}}{5}$=$\frac{1}{10}$.
故选D..
点评 本题考查几何概型,解题的关键是解不等式,确定其测度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.设集合A={x|x=2n,n∈N*},B={x${\;}^{\frac{1}{2}}$≤2},则A∩B=( )
| A. | {2} | B. | {2,4} | C. | {2,3,4} | D. | {1,2,3,4} |
19.已知全集U=R,集合A={x|x<1},则∁UA=( )
| A. | (-∞,1] | B. | [1,+∞) | C. | R | D. | (1,+∞) |
5.已知全集U=R,集合A={x|x(x-1)≥0},则∁UA=( )
| A. | [0,1] | B. | [1,+∞) | C. | (0,1) | D. | (-∞,0)∪(1,+∞) |
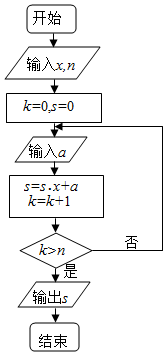 秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( )
秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( )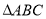 中,内角
中,内角 ,
,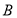 ,
, 所对的边分别为
所对的边分别为 ,
, ,
,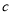 ,已知
,已知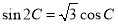 ,其中
,其中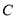 为锐角.
为锐角. 的大小;
的大小;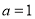 ,
, ,求边
,求边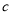 的长.
的长. B.
B.
 D.
D.