题目内容
已知向量
,
,
满足
-
+2
=0,且
⊥
,|
|=2,|
|=1,则|
|= .
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| a |
| c |
| b |
考点:向量的模
专题:平面向量及应用
分析:由于
⊥
,可得
•
=0.由于向量
,
,
满足
-
+2
=
,可得
=
+2
.再利用数量积的性质可得
2=(
+2
)2展开即可得出.
| a |
| c |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| b |
| a |
| c |
| b |
| a |
| c |
解答:
解:∵
⊥
,∴
•
=0.
∵向量
,
,
满足
-
+2
=
,∴
=
+2
.
∴
2=(
+2
)2=
2+4
•
+4
2=22+0+4×12=8.
∴|
|=2
.
故答案为:2
.
| a |
| c |
| a |
| c |
∵向量
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| b |
| a |
| c |
∴
| b |
| a |
| c |
| a |
| a |
| c |
| c |
∴|
| b |
| 2 |
故答案为:2
| 2 |
点评:本题考查了向量垂直于数量积的关系、数量积的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
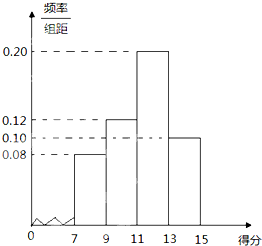 某中学高三年级共有学生1000人参加期中考试,今随机抽取50人,对本次考试数学卷第20题的得分情况进行统计,其频率分布直方图如图,在本年级中估计该题得分不低于11分的学生人数有
某中学高三年级共有学生1000人参加期中考试,今随机抽取50人,对本次考试数学卷第20题的得分情况进行统计,其频率分布直方图如图,在本年级中估计该题得分不低于11分的学生人数有