题目内容
如图,△ABC中,AC=BC=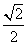 AB,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.
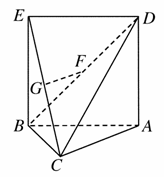
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V.
[解] (1)证明:连接AE,如下图所示.
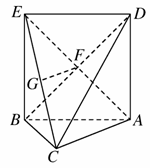
∵ADEB为正方形,
∴AE∩BD=F,且F是AE的中点,
又G是EC的中点,
∴GF∥AC,又AC⊂平面ABC,GF⊄平面ABC,
∴GF∥平面ABC.
(2)证明:∵ADEB为正方形,∴EB⊥AB,
又∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,EB⊂平面ABED,
∴BE⊥平面ABC,∴BE⊥AC.
又∵AC=BC=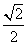 AB,
AB,
∴CA2+CB2=AB2,
∴AC⊥BC.
又∵BC∩BE=B,∴AC⊥平面BCE.
(3)取AB的中点H,连GH,∵BC=AC=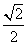 AB=
AB=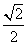 ,
,
∴CH⊥AB,且CH= ,又平面ABED⊥平面ABC
,又平面ABED⊥平面ABC
∴GH⊥平面ABCD,∴V=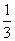 ×1×
×1× =
=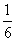 .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 (
( ,
, 为自然对数的底数).若曲线
为自然对数的底数).若曲线
 使得
使得 ,则实数
,则实数 的取值范围是____________.
的取值范围是____________. ,且
,且 ,则
,则 = .
= .  的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 上的射影
上的射影 为
为 的中点,则异面直线
的中点,则异面直线 与
与 所成的角的余弦值为( )
所成的角的余弦值为( )  B.
B. C.
C. D.
D.

 ( )
( ) B、
B、 C、
C、 D、
D、
 处的切线方程为( )
处的切线方程为( ) B、
B、
 D、
D、
 )
) 图象的一条对称轴是( )
图象的一条对称轴是( ) B.
B. C.
C. D.
D. 