题目内容
20．已知角α终边上一点P（m，1），cosα=-$\frac{1}{3}$．（1）求实数m的值；
（2）求tanα的值．
分析 由条件利用任意角的三角函数的定义，求得实数m的值、tanα的值．
解答 解：角α终边上一点P（m，1），cosα=$\frac{m}{\sqrt{{m}^{2}+1}}$=-$\frac{1}{3}$，∴m=-$\frac{\sqrt{2}}{4}$．
∴tanα=$\frac{1}{m}$=2$\sqrt{2}$．
点评 本题主要考查任意角的三角函数的定义，属于基础题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
15．
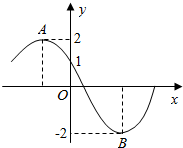如图为函数f（x）=Msin（ωx+φ）（M＞0，ω＞0，0≤φ≤π）的部分图象，若点A、B分别为函数f（x）的最高点与最低点，且|AB|=5，那么f（-1）=（ ）
如图为函数f（x）=Msin（ωx+φ）（M＞0，ω＞0，0≤φ≤π）的部分图象，若点A、B分别为函数f（x）的最高点与最低点，且|AB|=5，那么f（-1）=（ ）| A． | 2 | B． | $\sqrt{3}$ | C． | -$\sqrt{3}$ | D． | -2 |
12．已知P=$\frac{1}{{a}^{2}+a+1}$，Q=a2-a+1，则P、Q的大小关系为（ ）
| A． | P＞Q | B． | P＜Q | C． | P≤Q | D． | 无法确定 |
10．设a∈R，则“a=-1”是“直线l1：ax+2y-1=0与直线l2：x+（a-1）y-4=0平行”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |