题目内容
下列各式中正确的是( )
A、tan
| ||||
B、tan(-
| ||||
| C、tan4>tan3 | ||||
| D、tan 281°>tan 665° |
考点:三角函数线
专题:三角函数的图像与性质
分析:利用诱导公式化简各个选项中的正切,再比较出角的大小关系,利用正切函数的单调性判断出各个选项中的正切值的大小关系,即可判断出正误.
解答:
解:A、∵tan
=tan(π-
)=tan(-
),且-
<
,
由于y=tanx在(-
,
)单调递增,则tan
<tan
,A错;
B、∵tan(-
)=tan(-
-3π)=tan(-
),tan(-
)=tan(-3π-
)=tan(-
),
又-
>-
>-
,函数y=tanx在区间(-
,
)上是增函数,
∴tan(-
)>tan(-
),B错;
C、∵
<3<π<4<
,∴tan3<0,tan4>0,C正确;
D、∵tan 281°=tan(360°-79°)=tan(-79°),tan 665°=tan(720°-55°)=tan(-55°),
由于-79°<-55°,且函数y=tanx在区间(-90°,90°)上是增函数,
∴tan 281°<tan 665°,D错.
故选:C.
| 4π |
| 7 |
| 3π |
| 7 |
| 3π |
| 7 |
| 3π |
| 7 |
| 3π |
| 7 |
由于y=tanx在(-
| π |
| 2 |
| π |
| 2 |
| 4π |
| 7 |
| 3π |
| 7 |
B、∵tan(-
| 13π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 17π |
| 5 |
| 2π |
| 5 |
| 2π |
| 5 |
又-
| π |
| 4 |
| 2π |
| 5 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴tan(-
| 13π |
| 4 |
| 17π |
| 5 |
C、∵
| π |
| 2 |
| 3π |
| 2 |
D、∵tan 281°=tan(360°-79°)=tan(-79°),tan 665°=tan(720°-55°)=tan(-55°),
由于-79°<-55°,且函数y=tanx在区间(-90°,90°)上是增函数,
∴tan 281°<tan 665°,D错.
故选:C.
点评:本题主要考查诱导公式,正切函数的单调性的应用,注意三角函数值的符号,这是易错地方,属于中档题.

练习册系列答案
相关题目
曲线f(x)=xlnx+2在点x=1处的切线方程为( )
| A、y=2x+2 |
| B、y=2x-2 |
| C、y=x-1 |
| D、y=x+1 |
已知复数z=a+bi(a,b∈R),且|z-2|=
,则a、b满足的轨迹方程是( )
| 5 |
| A、(a-2)2+b2=5 |
| B、(a+2)2+b2=5 |
| C、a2+(b-2)2=5 |
| D、a2+(b+2)2=5 |
已知向量
=(3,1),
=(1,3),
=(k,7),若(
-
)∥
,则k=( )
| a |
| b |
| c |
| a |
| c |
| b |
| A、1 | B、3 | C、5 | D、7 |
设a>0,b>0,e是自然对数的底数,则( )
| A、若ea-3b=eb-2a,则a<b |
| B、若ea-3b=eb-2a,则a>b |
| C、若ea+3b=eb+2a,则a<b |
| D、若ea+3b=eb+2a,则a>b |
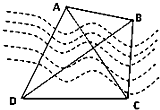 如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( )
如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( )A、
| ||||
B、200
| ||||
C、100
| ||||
| D、数据不够,无法计算 |
某校共有高中学生1000人,其中高一年级400人,高二年级340人,高三年级260人,现采用分层抽样抽取容量为50的样本,那么高一、高二、高三各年级抽取人数分别为( )
| A、20、17、13 |
| B、20、15、15 |
| C、40、34、26 |
| D、20、20、10 |