题目内容
某用人单位从甲、乙、丙、丁4名应聘者中招聘2人,若每名应聘者被录用的机会均等,则甲、乙2人中至少有1入被录用的概率为 _______.

【解析】
试题分析:事件甲、乙2人中至少有1入被录用的对立事件为甲、乙2人中皆不被录用,其概率为 ,因此甲、乙2人中至少有1入被录用的概率为
,因此甲、乙2人中至少有1入被录用的概率为
考点:古典概型概率

练习册系列答案
相关题目
(本小题满分13分)
现有两种投资方案,一年后投资盈亏的情况如下:
(1)投资股市:
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概 率 |
|
|
|
(2)购买基金:
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概 率 |
|
|
|
(Ⅰ)当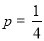 时,求q的值;
时,求q的值;
(Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于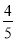 ,求
,求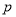 的取值范围;
的取值范围;
(Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知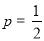 ,
,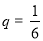 ,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.
,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.
 有两个极值点
有两个极值点 ,
, ,且
,且 ,则( )
,则( ) B.
B.
 D.
D.
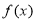 是定义在R上的奇函数,当
是定义在R上的奇函数,当 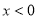 时
时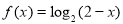 ,则
,则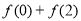 的值为_____.
的值为_____.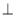 平面ABC.
平面ABC.
 BC,CP
BC,CP PB,求证:CP
PB,求证:CP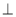 PA:
PA: ⊥平面ABC,求证:
⊥平面ABC,求证: //平面PBC.
//平面PBC. 满足
满足 ,则
,则 的最小值为_______.
的最小值为_______.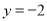 上有一个动点
上有一个动点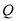 ,过点
,过点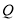 作直线
作直线 垂直于
垂直于 轴,动点
轴,动点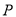 在
在 上,且满足
上,且满足 (
(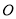 为坐标原点),记点
为坐标原点),记点 的轨迹为
的轨迹为 .
.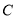 的方程;
的方程;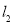 是曲线
是曲线 的一条切线,当点
的一条切线,当点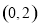 到直线
到直线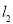 的距离最短时,求直线
的距离最短时,求直线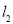 的方程.
的方程. 是平面内不共线的三点,点
是平面内不共线的三点,点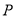 在该平面内且有
在该平面内且有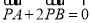 ,现将一粒黄豆随机
,现将一粒黄豆随机 内,则这粒黄豆落在
内,则这粒黄豆落在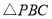 内的概率为___________.
内的概率为___________.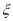 ,求
,求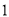 个新球的概率.
个新球的概率. 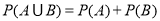 (事件
(事件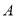 与事件
与事件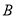 互斥).
互斥).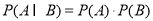 (事件
(事件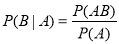 .
.




