题目内容
已知椭圆
的离心率为
，椭圆
的右焦点
和抛物线
的焦点相同.
（1）求椭圆的方程.
（2）如图，已知直线
与椭圆及抛物线
都有两个不同的公共点，且直线
与椭圆交于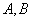
两点；过焦点的直线
与抛物线交于
两点，记
，求
的取值范围.
解：（1）椭圆的离心率
，抛物线的焦点为
，所以椭圆中的
，
，
.所以椭圆的方程为
. ……4分
（2）设
，
，
，则
由
消去
可得
（①），由
解得
或
；
由
消去可得
，由
解得
，所以。 …………………6分
由①可得
，
，
所以
…………………8分
当的斜率不存在时，
，此时， 
当的斜率存在时，设的方程为
，
，由由
消去可得
，所以
，
，所以，…………………10分
则
， 因为，所以
，所以
.…12分
练习册系列答案
相关题目
的解集为 ．
，α∈(0，
)，则cos(2α＋
)＝________.
的正方体
中，
为
的中点，
为
上任意一点，
为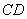
上任意两点，且
的长为定值，则下面的四个值中不为定值的是
的距离 B. 三棱锥
的体积 
与平面
所成的角 D.二面角
的大小 
的面积为__________.
为虚数单位，则
（ ）
B.
C.
D.
在区间
内是增函数，则实数
的取值范围是（ ）
B.
C . 
D. 
，
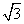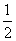)，离心率是
.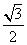