题目内容
10. 如图:在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点;
如图:在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点;(1)证明:EF∥平面PAD;
(2)求三棱锥E-ABC的体积;
(3)求EC与平面ABCD所成角的正切值.
分析 (1)证明EF∥AD,利用线面平行的判定定理,可得EF∥平面PAD;
(2)求出VP-ABCD,即可求三棱锥E-ABC的体积;
(3)取AB的中点G,连接EG,CG,则∠ECG为EC与平面ABCD所成角.
解答 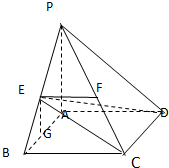 (1)证明:∵E,F分别是PB,PC的中点
(1)证明:∵E,F分别是PB,PC的中点
∴EF∥BC …(1分)
∵BC∥AD
∴EF∥AD …(2分)
∵AD?平面PAD,EF?平面PAD
∴EF∥平面PAD …(3分)
(2)解:∵AP=AB,BP=2,AP⊥平面ABCD
∴AB=AP=$\sqrt{2}$ …(4分)
∵S矩形ABCD=AB•BC=2$\sqrt{2}$
∴VP-ABCD=$\frac{1}{3}$S矩形ABCD•PA=$\frac{4}{3}$ …(5分)
∴三棱锥E-ABC的体积V=$\frac{1}{4}$VP-ABCD=$\frac{1}{3}$ …(6分)
(3)解:取AB的中点G,连接EG,CG,则∠ECG为EC与平面ABCD所成角,
∵EG=$\frac{\sqrt{2}}{2}$,CG=$\sqrt{4+\frac{1}{2}}$=$\frac{3\sqrt{2}}{2}$,
∴tan∠ECG=$\frac{1}{3}$.
点评 本小题主要考查直线与平面平行的判定、直线与平面垂直的性质、棱柱、棱锥、棱台的体积等基础知识,考查运算求解能力,考查空间想象力.属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
18.函数f(x)=sinxcosx是( )
| A. | 周期为π的偶函数 | B. | 周期为π的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为$\frac{π}{2}$的奇函数. |
5.函数$f(x)=\frac{1}{x}{log_3}(\sqrt{{x^2}-3x+2}+\sqrt{-{x^2}-3x+4})$的定义域为( )
| A. | (-∞,-4)∪[2,+∞) | B. | (-4,0)∪(0,1) | C. | (-4,0)∪(0,1) | D. | [-4,0)∪(0,1) |