题目内容
12. 已知三棱锥P-ABC,PA⊥平面ABC,AB=AC=AP,∠BAC=90°,D、E分别是AB,PC的中点,BF=2FC,△ABC是边长为2的等边三角形,O为它的中心,$PB=PC=\sqrt{2}$,D为PC的中点.
已知三棱锥P-ABC,PA⊥平面ABC,AB=AC=AP,∠BAC=90°,D、E分别是AB,PC的中点,BF=2FC,△ABC是边长为2的等边三角形,O为它的中心,$PB=PC=\sqrt{2}$,D为PC的中点.(1)求证:PD∥平面AEF;
(2)求AC与平面AEF所成角的正弦值.
分析 (1)取BF的中点G,连结DG、PG,DG∥AF,EF∥PG,从而平面PDG∥平面AEF,由此能证明PD∥平面AEF.
(2)取AC的中点H,连结EH,则EH⊥平面ABC,过H作HM⊥AF于M,连结EM,过H作HN⊥EM于N,连结AN,则∠HAN为AC于平面AEF所成的角,由此能求出AC与平面AEF所成角的正弦值.
解答  证明:(1)取BF的中点G,连结DG、PG,
证明:(1)取BF的中点G,连结DG、PG,
∵D是AB的中点,∴DG∥AF,又BF=2FC,∴F为CG的中点,
又E为PC的中点,∴EF∥PG,
又EF∩AF=F,∴平面PDG∥平面AEF,
∴PD∥平面AEF.
解:(2)取AC的中点H,连结EH,则EH⊥平面ABC,
过H作HM⊥AF于M,连结EM,
∴AF⊥平面EHM,∴平面AEF⊥平面EHM,
过H作HN⊥EM于N,即HN⊥平面AEF,
连结AN,则∠HAN为AC于平面AEF所成的角,
在等腰Rt△ABC中,设AC=1,则CF=$\frac{\sqrt{2}}{3}$,∠ACB=$\frac{π}{4}$,
∴AF=$\frac{\sqrt{5}}{3}$,cos$∠CAF=\frac{2\sqrt{5}}{5}$,即sin$∠CAF=\frac{\sqrt{5}}{5}$,
在Rt△AHM中,HM=AH•sin$∠CAF=\frac{\sqrt{5}}{10}$,
在Rt△EHM中,EH=$\frac{1}{2}$,EM=$\sqrt{E{H}^{2}+M{H}^{2}}$=$\frac{\sqrt{30}}{10}$,即HN=$\frac{EH×MH}{EM}=\frac{\sqrt{6}}{12}$,
在Rt△AHN中,sin∠HAN=$\frac{NH}{AH}$=$\frac{\sqrt{6}}{6}$,
∴AC与平面AEF所成角的正弦值为$\frac{\sqrt{6}}{6}$.
点评 本题考查线面平行的证明,考查线面所成角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )
已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )| A. | 8 | B. | 8+8$\sqrt{2}$ | C. | 8$\sqrt{2}$ | D. | 4+8$\sqrt{2}$ |

 如图,在正方体ABCD-A1B1C1D1中,求证:
如图,在正方体ABCD-A1B1C1D1中,求证: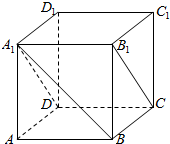 (1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明.
(1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明.