题目内容
20.设a∈R,则“a=2”是“直线l1:x+ay-a=0与直线l2:ax-(2a-3)y+1=0垂直”的( )| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要的条件 |
分析 对a分类讨论,利用两条直线相互垂直的充要条件即可得出.
解答 解:当a=0时,两条直线分别化为:x=0,4y+1=0,此时两条直线相互垂直;
当a=$\frac{3}{2}$时,此时两条直线不垂直,舍去;
当a≠0,$\frac{3}{2}$时,由于两条直线相互垂直,则$-\frac{1}{a}$×$\frac{a}{2a-3}$=-1,则a=2.
综上可得:a=0或2.
∴“a=2”是“直线l1:x+ay-a=0与直线l2:ax-(2a-3)y+1=0垂直”的充分不必要条件.
故选:A.
点评 本题考查了简易逻辑的判定方法、两条直线相互垂直的充要条件,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.若变量x,y满足约束条件$\left\{\begin{array}{l}y≤2x\\ x+y≥1\\ y≥-1\end{array}\right.$,则x+2y的最小值是( )
| A. | $-\frac{5}{2}$ | B. | 0 | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
8.在y轴上的截距为2,且与直线y=-3x-4垂直的直线的斜截式方程为( )
| A. | $y=\frac{1}{3}x+2$ | B. | $y=-\frac{1}{3}x-2$ | C. | y=-3x+2 | D. | y=3x-2 |
12.用最小二乘法计算利润额y对销售额x的回归直线方程,当销售额为4(千万元)时,估计利润额的大小( )
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
| A. | 2.3 | B. | 3.2 | C. | 4.2 | D. | 2.4 |
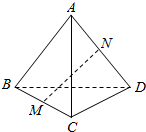 如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为30°或60°.
如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为30°或60°.