Question

若一个动点P(x，y)到两个定点A(-1，0)，A′(1，0)的距离和为定值m，试求P点的轨迹方程.

Answer 1

思路分析：定点到两定点的距离和为定值m，而两定点之间的距离是2，因此要分类考虑m与2的大小关系，其大小关系是我们解决问题的关键.

解：∵|PA|+|PA′|=m，|AA′|=2，|PA|+|PA′|≥|AA′|，∴m≥2.

(1)当m=2时，P点的轨迹就是线段AA′.∴其方程为y=0 (-1≤x≤1).

(2)当m＞2时，由椭圆的定义知，点P的轨迹是以A、A′为焦点的椭圆.

∵2c=2，2a=m，∴a=，c=1，b²=a²-c²=-1

.∴点P的轨迹方程为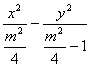=1.

    深化升华 平面内一动点到两定点的距离和等于常数时，动点的轨迹不一定是椭圆.当动点到两定点的距离和等于两定点之间的距离时，动点的轨迹是线段；当动点到两定点的距离和(常数)大于两定点之间的距离时，动点的轨迹是椭圆.