题目内容
6.若3cos($\frac{π}{2}$-θ)+cos(π+θ)=0,则cos2θ的值为( )| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
分析 先利用诱导公式化简,求得tanθ的值,再利用二倍角公式,即可求得结论.
解答 解:∵3cos($\frac{π}{2}$-θ)+cos(π+θ)=0,
∴3cos($\frac{π}{2}$-θ)+cos(π+θ)=3sinθ-cosθ=0,
则cosθ=3sinθ,
∴tanθ=$\frac{1}{3}$,
∴cos2θ=cos2θ-sin2θ=$\frac{co{s}^{2}θ-si{n}^{2}θ}{co{s}^{2}θ+si{n}^{2}θ}$=$\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{1-\frac{1}{9}}{1+\frac{1}{9}}$=$\frac{4}{5}$.
故选:A.
点评 本题考查二倍角的余弦,解题的关键是利用诱导公式化简,求得tanθ的值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.如图是某几何体的三视图,俯视图是边长为2的正三角形,则该几何体的体积是( )
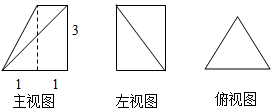

| A. | 4 | B. | 6 | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
15.若复数z满足$\frac{{{{(1-i)}^2}}}{z}$=1+i(i为虚数单位),则复数z位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图:在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
如图:在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3. 四棱锥P-ABCD中,点P在平面ABCD内的射影H在棱AD上,PA⊥PD,底面ABCD是梯形,BC∥AD,AB⊥AD,且AB=BC=1,AD=2.
四棱锥P-ABCD中,点P在平面ABCD内的射影H在棱AD上,PA⊥PD,底面ABCD是梯形,BC∥AD,AB⊥AD,且AB=BC=1,AD=2. 已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为菱形,且∠DAB=$\frac{π}{3}$.
已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为菱形,且∠DAB=$\frac{π}{3}$.