题目内容
正六棱锥P-ABCDEF中，G为PB的中点，则三棱锥D-GAC与三棱锥P-GAC体积之比为
- A.1：1
- B.1：2
- C.2：1
- D.3：2
C
分析：由于G是PB的中点，故P-GAC的体积等于B-GAC的体积；求出DH=2BH，即可求出三棱锥D-GAC与三棱锥P-GAC体积之比．
解答：由于G是PB的中点，故P-GAC的体积等于B-GAC的体积
在底面正六边形ABCDER中
BH=ABtan30°=
AB
而BD=
AB
故DH=2BH
于是VD-GAC=2VB-GAC=2VP-GAC
故选C．
点评：本题考查棱锥的体积计算，考查转化思想，是基础题．
分析：由于G是PB的中点，故P-GAC的体积等于B-GAC的体积；求出DH=2BH，即可求出三棱锥D-GAC与三棱锥P-GAC体积之比．
解答：由于G是PB的中点，故P-GAC的体积等于B-GAC的体积
在底面正六边形ABCDER中
BH=ABtan30°=
AB而BD=
AB故DH=2BH
于是VD-GAC=2VB-GAC=2VP-GAC
故选C．
点评：本题考查棱锥的体积计算，考查转化思想，是基础题．
练习册系列答案
相关题目
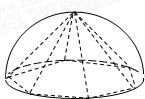如图，半径为R的半球内有一内接正六棱锥P-ABCDEF，则直线PA与平面BPE所成角正弦值是
（2007•广州模拟）如图，半径为2的半球内有一内接正六棱锥P-ABCDEF，则此正六棱锥的体积为（ ）