题目内容
9.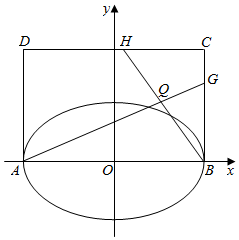 如图,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴端点,四边形ABCD为矩形,且AD=2b,H、G分别在线段DC、BC上,BH与AG相交于Q,且$\overrightarrow{BG}=λ\overrightarrow{BC}$,$\overrightarrow{CH}=μ\overrightarrow{CD}$.
如图,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴端点,四边形ABCD为矩形,且AD=2b,H、G分别在线段DC、BC上,BH与AG相交于Q,且$\overrightarrow{BG}=λ\overrightarrow{BC}$,$\overrightarrow{CH}=μ\overrightarrow{CD}$.(1)若AB=8,离心率为$\frac{\sqrt{2}}{2}$;
①求椭圆的方程;
②若$λ=\frac{3}{4}$,且Q点在AB为直径的圆上,求μ的值;
(2)若λ=μ,试判断点Q是否在椭圆上,请说明理由.
分析 (1)①由题意可得a=4,运用菱形公式可得b=c=2$\sqrt{2}$,进而得到椭圆方程;
②Q点在AB为直径的圆上,可得∠AQB=90°,即有tan∠GAB•tan∠BHC=1,运用直角三角形中正切函数的定义,解方程即可得到所求值;
(2)求得G(a,2λb),CH=2aλ,可得H(a-2aλ,2b),又A(-a,0),B(a,0),求得AG和BH的方程,解得Q的坐标,代入椭圆方程,即可判断在椭圆上.
解答 解:(1)①由题意可得2a=8,即a=4,
e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,可得b=c=2$\sqrt{2}$,
可得椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{8}$=1;
②Q点在AB为直径的圆上,可得∠AQB=90°,
即有tan∠GAB•tan∠BHC=1,
即有$\frac{BG}{AB}$•$\frac{BC}{CH}$=1,即$\frac{\frac{3}{4}•4\sqrt{2}}{8}$•$\frac{4\sqrt{2}}{8μ}$=1,
解得μ=$\frac{3}{8}$;
(2)λ=μ,即有G(a,2λb),
CH=2aλ,可得H(a-2aλ,2b),
又A(-a,0),B(a,0),
可得直线AG的方程为y=$\frac{λb}{a}$(x+a),
BH的方程为y=-$\frac{b}{λa}$(x-a),
解方程组可得Q($\frac{a(1-{λ}^{2})}{1+{λ}^{2}}$,$\frac{2bλ}{1+{λ}^{2}}$),
代入椭圆方程的左边可得:
$\frac{(1-{λ}^{2})^{2}}{(1+{λ}^{2})^{2}}$+$\frac{4{λ}^{2}}{(1+{λ}^{2})^{2}}$=$\frac{1+2{λ}^{2}+{λ}^{4}}{(1+{λ}^{2})^{2}}$=1.
即有Q在椭圆上.
点评 本题考查椭圆的方程的求法,注意运用离心率公式,考查向量共线的坐标表示和共线定理,同时考查直线的交点的求法,以及点与椭圆的位置关系的判断,属于中档题.

| 分数段 | (0,80) | [80,110) | [110,150) |
| 频数 | 35 | 50 | 15 |
| 平均成绩 | 60 | 98 | 130 |
| A. | 若“p∧(?q)”为真命题,则“p∧q”也为真命题 | |
| B. | “x=3”是“2x2-7x+3=0”成立的充分不必要条件 | |
| C. | 命题“?x∈R,均有x2-x+1>0”的否定是:“?x∈R,使得x2-x+1<0” | |
| D. | 线性回归方程$\hat y=\hat bx+\hat a$对应的直线一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点 |
| A. | x2+$\frac{{y}^{2}}{3}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | y2+$\frac{{x}^{2}}{3}$=1 | D. | y2-$\frac{{x}^{2}}{3}$=1 |
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
| A. | $(-∞,-\frac{1}{3})$ | B. | $(-\frac{1}{3},+∞)$ | C. | $(\frac{1}{3},+∞)$ | D. | $(-∞,\frac{1}{3})$ |