题目内容
在△ABC中,sinA:sinB:sinC=3:4:5,则cosC的值为( )
A.
| B.-
| C.0 | D.
|
∵在△ABC中,sinA:sinB:sinC=3:4:5,
∴根据正弦定理,得a:b:c=3:4:5,
因此设a=3x,b=4x,c=5x,x>0,
可得cosC=
=
=0
故选:C
∴根据正弦定理,得a:b:c=3:4:5,
因此设a=3x,b=4x,c=5x,x>0,
可得cosC=
| a2+b2-c2 |
| 2ab |
| 9x2+16x2-25x2 |
| 2•3x•4x |
故选:C

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
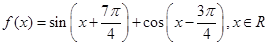 .
.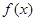 的最小正周期和最值;
的最小正周期和最值;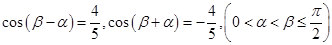 , 求证:
, 求证: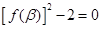 .
.