题目内容
在直角坐标系xOy中,以O为极点,x轴非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos(θ-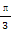
)=1,M,N分别为C与x轴,y轴的交点.
(1)写出C的直角坐标方程,并求M,N的极坐标.
(2)设MN的中点为P,求直线OP的极坐标方程.
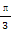)=1,M,N分别为C与x轴,y轴的交点.(1)写出C的直角坐标方程,并求M,N的极坐标.
(2)设MN的中点为P,求直线OP的极坐标方程.
(1) 
x+
y=1 M(2,0) N(
,
) (2) θ=
(ρ∈R)
x+y=1 M(2,0) N(,) (2) θ=(ρ∈R)(1)由ρcos(θ-
)=1得
ρ(cosθ+sinθ)=1.
从而C的直角坐标方程为x+y=1.
即x+
y=2.
当θ=0时,ρ=2,所以M(2,0);
当θ=时,ρ=,所以N(,).
(2)M点的直角坐标为(2,0),N点的直角坐标为(0,),所以P点的直角坐标为(1,
),则P点的极坐标为(,).
所以直线OP的极坐标方程为θ=(ρ∈R).
)=1得ρ(
cosθ+sinθ)=1.从而C的直角坐标方程为
x+y=1.即x+
y=2.当θ=0时,ρ=2,所以M(2,0);
当θ=
时,ρ=,所以N(,).(2)M点的直角坐标为(2,0),N点的直角坐标为(0,
),所以P点的直角坐标为(1,),则P点的极坐标为(,).所以直线OP的极坐标方程为θ=
(ρ∈R).
练习册系列答案
相关题目
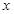轴的正半轴重合，且两坐标系有相同的长度单位，圆C的参数方程为
（
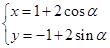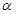为参数），点Q的极坐标为
。
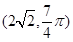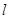过点Q且与圆C交于M，N两点，求当弦MN的长度为最小时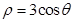，直线
被直线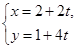
(
是参数)截得的弦长．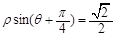
，则极点到这条直线的距离是 ．
（
为参数且
）与曲线
（
是参数且
），则直线
与曲线
的交点坐标为 .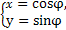
(φ为参数),曲线C2的参数方程为
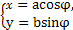(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=
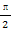时,这两个交点重合.
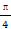时,l与C1,C2的交点分别为A1,B1,当α=-
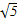,求a的值.
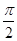(ρ∈R)和ρcos θ＝2
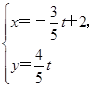(t为参数)．