题目内容
在数列{![]() }中,
}中,![]() ,并且对任意
,并且对任意![]() 都有
都有![]() 成立,令
成立,令![]() .
.
(Ⅰ)求数列{![]() }的通项公式;
}的通项公式;
(Ⅱ)求数列{![]() }的前n项和
}的前n项和![]() .
.
解:(1)当n=1时,![]() ,当
,当![]() 时,
时,
由![]() 得
得![]() 所以
所以![]()
所以数列![]() 是首项为3,公差为1的等差数列,
是首项为3,公差为1的等差数列,
所以数列![]() 的通项公式为
的通项公式为![]()
(2)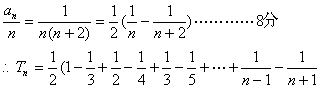
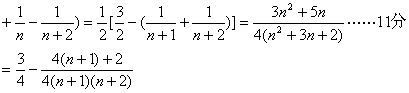

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
题目内容
在数列{![]() }中,
}中,![]() ,并且对任意
,并且对任意![]() 都有
都有![]() 成立,令
成立,令![]() .
.
(Ⅰ)求数列{![]() }的通项公式;
}的通项公式;
(Ⅱ)求数列{![]() }的前n项和
}的前n项和![]() .
.
解:(1)当n=1时,![]() ,当
,当![]() 时,
时,
由![]() 得
得![]() 所以
所以![]()
所以数列![]() 是首项为3,公差为1的等差数列,
是首项为3,公差为1的等差数列,
所以数列![]() 的通项公式为
的通项公式为![]()
(2)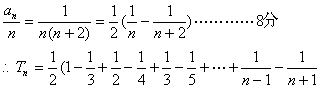
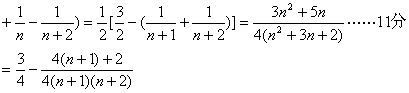

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案