题目内容
过点P(2,1)的直线l与x轴、y轴的正半轴交于A、B两点,O为坐标原点,当S△AOB最小时,求直线l的方程.
解:设直线l的方程为y-1=k(x-2),
由题意知k<0.
令x=0,则y=1-2k,即B点坐标为(0,1-2k);
令y=0,则x=2-![]() ,即A点坐标为(2-
,即A点坐标为(2-![]() ,0).
,0).
∴S△AOB=![]() |2-
|2-![]() |·|1-2k|
|·|1-2k|
=![]() (2-
(2-![]() )(1-2k)
)(1-2k)
=![]() (4-4k-
(4-4k-![]() )
)
≥![]() |4+2
|4+2![]() |
|
=![]() (4+4)=4.
(4+4)=4.
当且仅当-4k=-![]() 时,上式取“=”.
时,上式取“=”.
此时k2=![]() ,k=±
,k=±![]() .
.
又k<0,∴k=-![]() .
.
∴直线方程为y-1=-![]() (x-2),
(x-2),
即x+2y-4=0.

练习册系列答案
相关题目

 椭圆E:
椭圆E: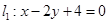 与
与 的交点为P,直
的交点为P,直 的方程为:
的方程为: .
. 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直 ,原点到该直线的距离为
,原点到该直线的距离为 .
. 求直线MN的方程;
求直线MN的方程; 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。