题目内容
14.5位同学报名参加学校的篮球队、足球队和羽毛球队,要求每位同学只能选报一个球队,则所有的报名数有( )| A. | 53 | B. | 35 | C. | $A_5^3$ | D. | 5! |
分析 根据题意,易得5名同学中每人有3种报名方法,由分步计数原理计算可得答案.
解答 解:5位同学报名参加学校的篮球队、足球队和羽毛球队,每人限报一项,
每人有3种报名方法;
根据分步计数原理,可得共有3×3×3×3×3=35种不同的报名方法;
故选B.
点评 本题考查分步计数原理的运用,解题时注意题干条件中“每人限报一项”.

练习册系列答案
相关题目
5.函数f(x)=|x|+1是( )
| A. | 在(0,+∞)上单调递增的奇函数 | B. | 在(0,+∞)上单调递减的奇函数 | ||
| C. | 在(0,+∞)上单调递增的偶函数 | D. | 在(0,+∞)上单调递减的偶函数 |
3.设数列{an}是等差数列,且a4=-4,a9=4,Sn是数列{an}的前n项和,则( )
| A. | S5<S6 | B. | S5=S6 | C. | S7=S5 | D. | S7=S6. |
4.如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖块数为( )
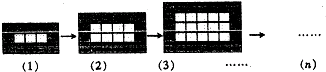

| A. | 4n+2 | B. | 4n+4 | C. | 4n+6 | D. | 4n+8 |
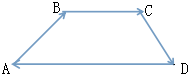 如图所示的四边形ABCD,已知$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(x,y),$\overrightarrow{CD}$=(-2,-3)
如图所示的四边形ABCD,已知$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(x,y),$\overrightarrow{CD}$=(-2,-3)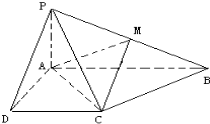 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.