题目内容
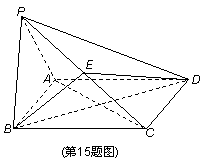
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,
BP=BC,E为PC的中点.
(1)求证:AP∥平面BDE;
(2)求证:BE⊥平面PAC.
 |
证:(1)设AC∩BD=O,连结OE.
因为ABCD为矩形,所以O是AC的中点.
因为E是PC中点,所以OE∥AP.
因为AP 平面BDE,OE
平面BDE,OE 平面BDE,
平面BDE,
所以AP∥平面BDE.
(2)因为平面PAB⊥平面ABCD,BC⊥AB,平面PAB∩平面ABCD=AB,
所以BC⊥平面PAB.
因为AP 平面PAB,所以BC⊥PA.
平面PAB,所以BC⊥PA.
因为PB⊥PA,BC∩PB=B,BC,PB 平面PBC,
平面PBC,
所以PA⊥平面PBC.
因为BE 平面PBC,所以PA⊥BE.
平面PBC,所以PA⊥BE.
因为BP=PC,且E为PC中点,所以BE⊥PC.
因为PA∩PC=P,PA,PC 平面PAC,
平面PAC,
所以BE⊥平面PAC.

练习册系列答案
相关题目
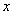 ,
,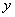 满足约束条件
满足约束条件 且目标函数
且目标函数 的最大值是6,最小值是1,则
的最大值是6,最小值是1,则 的值是 ( )
的值是 ( )  的图象向右平移
的图象向右平移 单位后与函数
单位后与函数 的图象重合,则
的图象重合,则
 (B)
(B)
 (D)
(D)
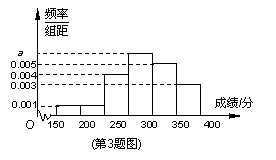
 |=1,|
|=1,| |=2,∠AOB=
|=2,∠AOB= ,
, =
=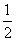

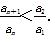 .
. ,
, ,则
,则 .
.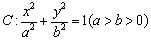 的左、右焦点分别为
的左、右焦点分别为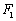 、
、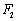 ,过
,过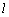 与椭圆
与椭圆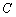 交于点
交于点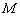 、
、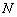 .
.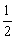 ,右准线的方程为
,右准线的方程为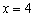 ,
,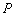 ,求
,求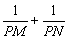 的
的 值;
值;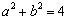 时,设
时,设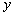 轴于点
轴于点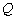 ,
,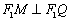 ,证明:点
,证明:点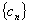 中,所有满足
中,所有满足 的正整数
的正整数 的个数称为这个数列
的个数称为这个数列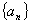 的前
的前 项和
项和 ,
, (
( ),则数列
),则数列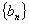 的变号数为 .
的变号数为 .