题目内容
如图,A,B是海面上位于东西方向相距5(3+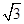 )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20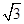 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?

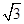 )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20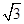 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
1小时
解:由题意知AB=5(3+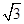 )海里,
)海里,
∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30°)=105°.
在△ADB中,由正弦定理得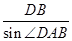 =
=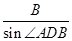 ,
,
∴DB=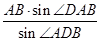 =
=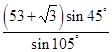 =
= =10
=10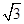 (海里).
(海里).
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20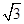 (海里),
(海里),
在△DBC中,由余弦定理得
CD2=BD2+BC2-2BD·BC·cos∠DBC=300+1200-2×10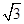 ×20
×20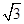 ×
×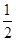 =900,
=900,
∴CD=30(海里),则需要的时间t=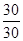 =1(小时),
=1(小时),
答:救援船到达D点需要1小时.
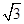 )海里,
)海里,∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30°)=105°.
在△ADB中,由正弦定理得
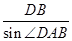 =
=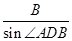 ,
,∴DB=
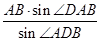 =
=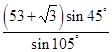 =
= =10
=10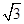 (海里).
(海里).又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20
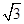 (海里),
(海里),在△DBC中,由余弦定理得
CD2=BD2+BC2-2BD·BC·cos∠DBC=300+1200-2×10
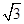 ×20
×20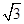 ×
×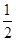 =900,
=900,∴CD=30(海里),则需要的时间t=
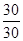 =1(小时),
=1(小时),答:救援船到达D点需要1小时.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
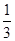 ,求B.
,求B.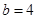 ,
,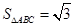 ,则
,则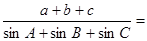 .
.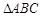 中,角
中,角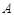 ,
,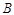 ,
,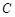 所对的边分别是
所对的边分别是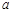 ,
,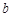 ,
,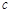 ,已知
,已知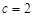 ,
,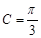 .
.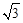 ,求
,求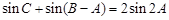 ,求
,求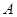 、
、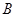 、
、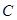 分别为
分别为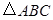 的三边
的三边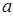 、
、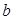 、
、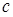 所对的角,向量
所对的角,向量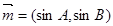 ,
,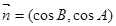 ,且
,且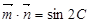 .
.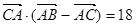 ,求边
,求边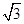 sinA-cos(B+
sinA-cos(B+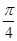 )的最大值为( )
)的最大值为( )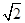
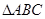 三个内角
三个内角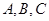 满足
满足 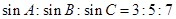 ,则此三角形内角的最大值为 .
,则此三角形内角的最大值为 .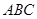 中,
中,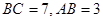 ,且
,且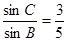 .
.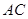 ; (2)求
; (2)求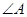 .
.