题目内容
8.等比数列{an}的前n项和为Sn,a1+a2+a3=26,S6=728.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:${{S}_{n+1}}^{2}-{S}_{n}{S}_{n+2}=4×{3}^{n}$.
分析 (Ⅰ)设等比数列{an}的公比为q,从而可得$\left\{\begin{array}{l}{S_3}=\frac{{{a_1}({1-{q^3}})}}{1-q}=26\\{S_6}=\frac{{{a_1}({1-{q^6}})}}{1-q}=728\end{array}\right.$,从而解方程即可;
(Ⅱ)由(Ⅰ)可得${S_n}=\frac{{2×({1-{3^n}})}}{1-3}={3^n}-1$,从而写出${S_{n+1}}={3^{n+1}}-1$,${S_{n+2}}={3^{n+2}}-1$,从而证明.
解答 解:(Ⅰ)设等比数列{an}的公比为q,
由728≠2×26得S6≠2S3,
故q≠1,
故$\left\{\begin{array}{l}{S_3}=\frac{{{a_1}({1-{q^3}})}}{1-q}=26\\{S_6}=\frac{{{a_1}({1-{q^6}})}}{1-q}=728\end{array}\right.$,
解得$\left\{\begin{array}{l}{a_1}=2\\ q=3\end{array}\right.$,
∴${a_n}=2×{3^{n-1}}$.
(Ⅱ)证明:由(Ⅰ)可得,${S_n}=\frac{{2×({1-{3^n}})}}{1-3}={3^n}-1$;
∴${S_{n+1}}={3^{n+1}}-1$,${S_{n+2}}={3^{n+2}}-1$,
∴${S_{n+1}}^2-{S_{n+2}}{S_n}=4×{3^n}$.
点评 本题考查了等比数列的性质应用及前n项和公式的应用.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
18.已知全集U={x|-1<x<3},集合A={x|x2-3x<0},则∁UA=( )
| A. | {x|-1<x≤0} | B. | {x|-1<x<3} | C. | {x|0<x<3} | D. | {x|x≤0或x≥3} |
19.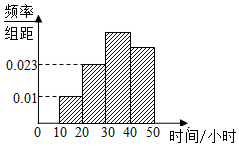 为了了解学生参加体育锻炼的情况,现抽取了n名学生进行调查,结果显示这些学生每月的锻炼时间(单位:小时)都在[10,50],其中锻炼时间在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了了解学生参加体育锻炼的情况,现抽取了n名学生进行调查,结果显示这些学生每月的锻炼时间(单位:小时)都在[10,50],其中锻炼时间在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
 为了了解学生参加体育锻炼的情况,现抽取了n名学生进行调查,结果显示这些学生每月的锻炼时间(单位:小时)都在[10,50],其中锻炼时间在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了了解学生参加体育锻炼的情况,现抽取了n名学生进行调查,结果显示这些学生每月的锻炼时间(单位:小时)都在[10,50],其中锻炼时间在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )| A. | 150 | B. | 160 | C. | 180 | D. | 200 |
13.如图是某样本数据的茎叶图,则该样本的中位数、众数、极差分别是( )


| A. | 32 34 32 | B. | 33 45 35 | C. | 34 45 32 | D. | 33 36 35 |
17.在△ABC中,若A=44°,a=18,b=24,则此三角形解的情况为( )
| A. | 无解 | B. | 一解 | C. | 两解 | D. | 不能确定 |
18.设关于x,y的不等式组$\left\{\begin{array}{l}{x+y≥1}\\{x-2y≥t}\\{3x-2y≤3}\end{array}\right.$,表示的平面区域内存在点M(x0,y0),满足x0+2y0=5,则实数t的取值范围是( )
| A. | (-∞,-1] | B. | [1,+∞) | C. | (-∞,1] | D. | 以上都不正确 |
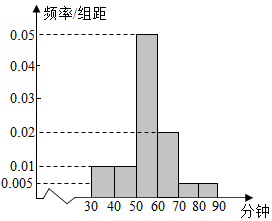 某学校高二年级共有女生300人,现调查她们每天的课外运动时间,发现她们的课外运动时间介于30分钟到90分钟之间,如图是统计结果的频率分布直方图,则她们的平均运动时间大约是56.5分钟.
某学校高二年级共有女生300人,现调查她们每天的课外运动时间,发现她们的课外运动时间介于30分钟到90分钟之间,如图是统计结果的频率分布直方图,则她们的平均运动时间大约是56.5分钟.