Question

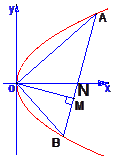
设点A和B为抛物线 y²=4px(p＞0)上原点以外的两个动点，已知OA⊥OB，OM⊥AB，求点M的轨迹方程，并说明它表示什么曲线.

Answer 1

动点M的轨迹方程为x²+y²－4px=0(x≠0)，它表示以(2p,0)为圆心，以2p为半径的圆，去掉坐标原点.

解析:

解法一:设A(x₁,y₁),B(x₂,y₂),M(x,y) (x≠0)

直线AB的方程为x=my+a

由OM⊥AB，得m=－

由y²=4px及x=my+a，消去x,得y²－4pmy－4pa=0

所以y₁y₂=－4pa, x₁x₂=

所以，由OA⊥OB，得x₁x₂ =－y₁y₂

所以

故x=my+4p,用m=－代入，得x²+y²－4px=0(x≠0)

故动点M的轨迹方程为x²+y²－4px=0(x≠0)，它表示以(2p,0)为圆心，以2p为半径的圆，去掉坐标原点.

解法二：设OA的方程为，代入y²=4px得

则OB的方程为，代入y²=4px得

∴AB的方程为，过定点，

由OM⊥AB，得M在以ON为直径的圆上（O点除外）

故动点M的轨迹方程为x²+y²－4px=0(x≠0)，它表示以(2p,0)为圆心，以2p为半径的圆，去掉坐标原点.

解法三: 设M(x,y) (x≠0)，OA的方程为，

代入y²=4px得

则OB的方程为，代入y²=4px得

由OM⊥AB，得

M既在以OA为直径的圆：……①上，

又在以OB为直径的圆： ……②上（O点除外），

①+②得 x²+y²－4px=0(x≠0)

故动点M的轨迹方程为x²+y²－4px=0(x≠0)，它表示以(2p,0)为圆心，以2p为半径的圆，去掉坐标原点.