题目内容
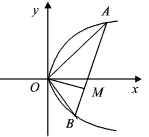
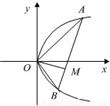
如图，设点A和B为抛物线y2=4px（p＞0）上原点以外的两个动点，已知OA⊥OB，OM⊥AB．求点M的轨迹方程，并说明它表示什么曲线．
分析：由OA⊥OB可得A、B两点的横坐标之积和纵坐标之积均为定值，由OM⊥AB可用斜率处理，得到M的坐标和A、B坐标的联系，再注意到M在AB上，由以上关系即可得到M点的轨迹方程；此题还可以考虑设出直线AB的方程解决．
解答：解：如图，点A，B在抛物线y2=4px上，
设A(
，yA)，B(
，yB)，OA、OB的斜率分别为kOA、kOB．
∴kOA=
=
，kOB=
由OA⊥AB，得kOA•kOB=
=-1①
依点A在AB上，得直线AB方程
(yA+yB)(y-yA)=4p(x-
)②
由OM⊥AB，得直线OM方程y=
x③
设点M（x，y），则x，y满足②、③两式，将②式两边同时乘以-
，
并利用③式整理得
y2A+yyA-(x2+y2)=0④
由③、④两式得
-
yAyB-(x2+y2)=0
由①式知，yAyB=-16p2
∴x2+y2-4px=0
因为A、B是原点以外的两点，所以x＞0
所以M的轨迹是以（2p，0）为圆心，以2p为半径的圆，去掉坐标原点．
设A(
| y2A |
| 4p |
| y2B |
| 4p |
∴kOA=
| yA | ||
|
| 4p |
| yA |
| 4p |
| yB |
由OA⊥AB，得kOA•kOB=
| 16p2 |
| yAyB |
依点A在AB上，得直线AB方程
(yA+yB)(y-yA)=4p(x-
| y2A |
| 4p |
由OM⊥AB，得直线OM方程y=
| yA+yB |
| -4p |
设点M（x，y），则x，y满足②、③两式，将②式两边同时乘以-
| x |
| 4p |
并利用③式整理得
| x |
| 4p |
由③、④两式得
-
| x |
| 4p |
由①式知，yAyB=-16p2
∴x2+y2-4px=0
因为A、B是原点以外的两点，所以x＞0
所以M的轨迹是以（2p，0）为圆心，以2p为半径的圆，去掉坐标原点．
点评：本小题主要考查直线、抛物线的基础知识，考查由动点求轨迹方程的基本方法以及方程化简的基本技能．
练习册系列答案
相关题目
（p>0）上原点以外的两个动点，已知OA⊥OB，OM⊥AB.求点M的轨迹方程，并说明它表示什么曲线. 
