题目内容
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.罗庄区2014年3月6日至15日每天的PM2.5监测数据如茎叶图所示.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.罗庄区2014年3月6日至15日每天的PM2.5监测数据如茎叶图所示.(Ⅰ)小王在此期间也有两天经过此地,这两天此地PM2.5监测数据均未超标.请计算出这两天空气质量恰好有一天为一级的概率;
(Ⅱ)从所给10天的数据中任意抽取三天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列及期望.
考点:离散型随机变量的期望与方差,茎叶图
专题:概率与统计
分析:(Ⅰ)利用古典概型概率计算公式能求出这两天空气质量恰好有一天为一级的概率.
(Ⅱ)ξ的可能值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及期望.
(Ⅱ)ξ的可能值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及期望.
解答:
解:(Ⅰ)记“这两天此地PM2.5监测数据均未超标且空气质量恰好有一天为一级”为事件A,
P(A)=
=
.…(4分)
(Ⅱ)ξ的可能值为0,1,2,3,…(5分)
P(ξ=0)=
=
,P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,…(9分)
其分布列为:
Eξ=0×
+1×
+2×
+3×
=
.…(12分)
P(A)=
| ||||
|
| 8 |
| 15 |
(Ⅱ)ξ的可能值为0,1,2,3,…(5分)
P(ξ=0)=
| ||
|
| 1 |
| 6 |
| ||||
|
| 1 |
| 2 |
P(ξ=2)=
| ||||
|
| 3 |
| 10 |
P(ξ=3)=
| ||
|
| 1 |
| 30 |
其分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 6 |
| 1 |
| 2 |
| 3 |
| 10 |
| 1 |
| 30 |
| 6 |
| 5 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
相关题目
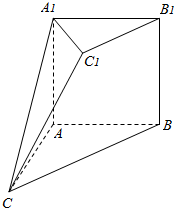 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=