题目内容
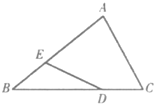
如图，△ABC中，
=2
，
=2
，设
=
，
=
，则
= ．
| AE |
| EB |
| BD |
| DC |
| AB |
| a |
| AC |
| b |
| DE |
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：由∵△ABC中，
=2
，
=2
，利用向量加法的三角形法则和平行四边形法则，可得
=
+
=
+
=
(
-
)-
=
+
，进而得到答案．
| AE |
| EB |
| BD |
| DC |
| DE |
| DB |
| BE |
| 2 |
| 3 |
| CB |
| 1 |
| 3 |
| BA |
| 2 |
| 3 |
| AB |
| AC |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
解答：
解：∵△ABC中，
=2
，
=2
，
=
，
=
，
∴
=
+
=
+
=
(
-
)-
=
+
=
+
．
故答案为：
+
| AE |
| EB |
| BD |
| DC |
| AB |
| a |
| AC |
| b |
∴
| DE |
| DB |
| BE |
| 2 |
| 3 |
| CB |
| 1 |
| 3 |
| BA |
| 2 |
| 3 |
| AB |
| AC |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
故答案为：
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
点评：本题考查两个向量的加法和减法法则，以及共线向量的表示方法，体现了数形结合的数学思想．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图所示，某小区为美化环境，准备在小区内草坪的一侧修建一条直路OC；另一侧修建一条休闲大道，它的前一段OD是函数y=k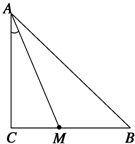
已知等腰Rt△ABC中，∠C=90°．
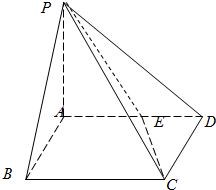在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为正方形，且PA=AD=2，E为棱AD的中点．